6.1 The Normal Curve

EXAMPLE 6.1

In this section, we learn more about the normal curve through a real-life example. Let’s examine the heights, in inches, of a sample of 5 students taken from a larger sample of the authors’ statistics students:

52 77 63 64 64

Figure 6-2 shows a histogram of those heights, with a normal curve superimposed on the histogram. With so few scores, we can only begin to guess at the emerging shape of a normal distribution. Notice that three of the observations (63 inches, 64 inches, and 64 inches) are represented by the middle bar. This is why it is three times higher than the bars that represent a single observation of 52 inches and another observation of 77 inches.

image
Figure 6.2: FIGURE 6-2
Sample of 5
Here is a histogram of the heights in inches of 5 students. With so few students, the data are unlikely to closely resemble the normal curve that we would see for an entire population of heights.

Now, here are the heights in inches from a sample of 30 students:

52 77 63 64 64 62 63 64 67 52
67 66 66 63 63 64 62 62 64 65
67 68 74 74 69 71 61 61 66 66

127

Figure 6-3 shows the histogram for these data. Notice that the heights of 30 students resemble a normal curve more so than do the heights of just 5 students, although certainly they don’t match it perfectly.

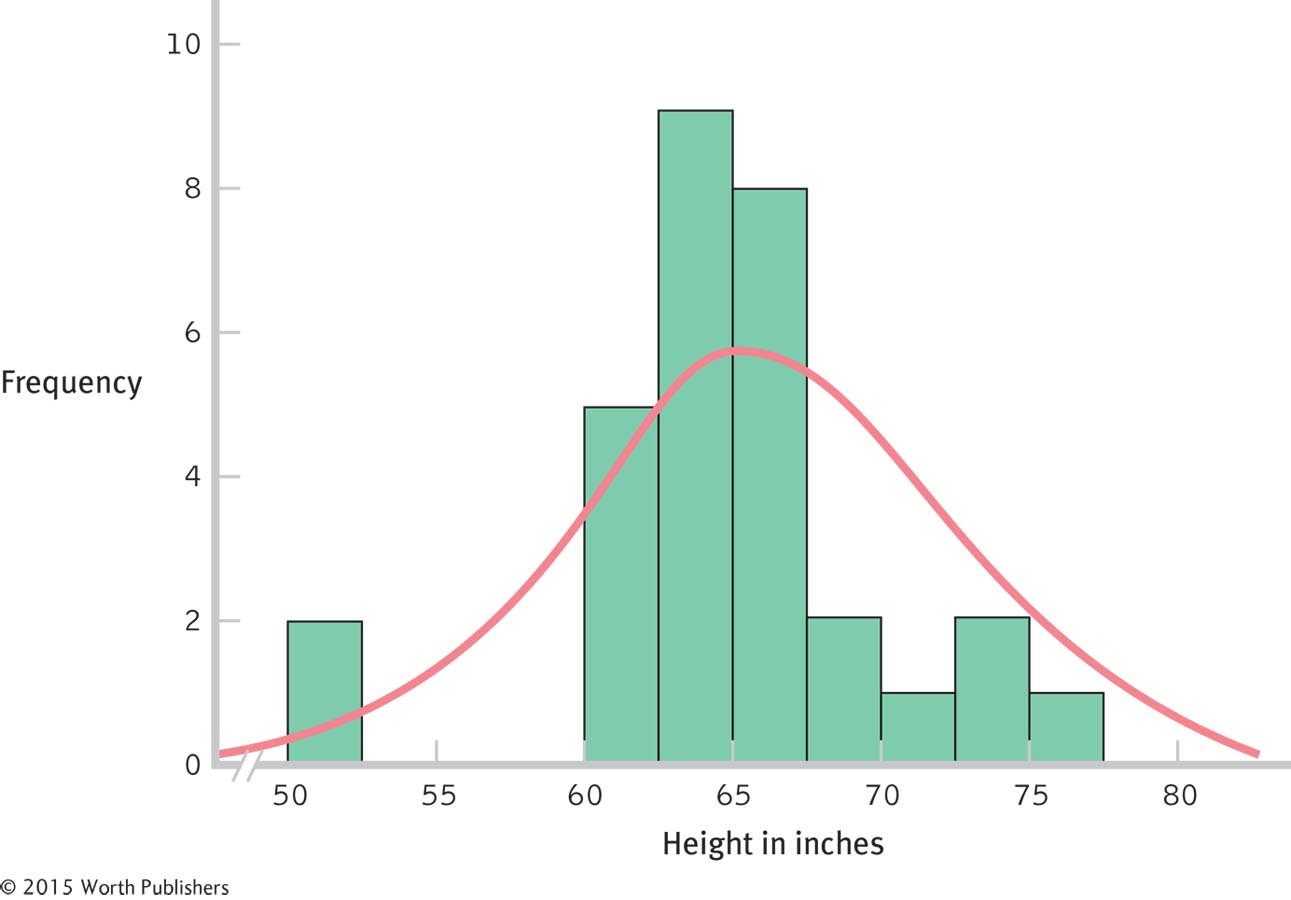
image
Figure 6.3: FIGURE 6-3
Sample of 30
Here is a histogram of the heights in inches of 30 students. With a larger sample, the data begin to resemble the normal curve of an entire population of heights.

MASTERING THE CONCEPT

6-1: The distributions of many variables approximate a normal curve, a mathematically defined, bell-shaped curve that is unimodal and symmetric.

Table 6-1 gives the heights in inches from a random sample of 140 students. Figure 6-4 shows the histogram for these data.

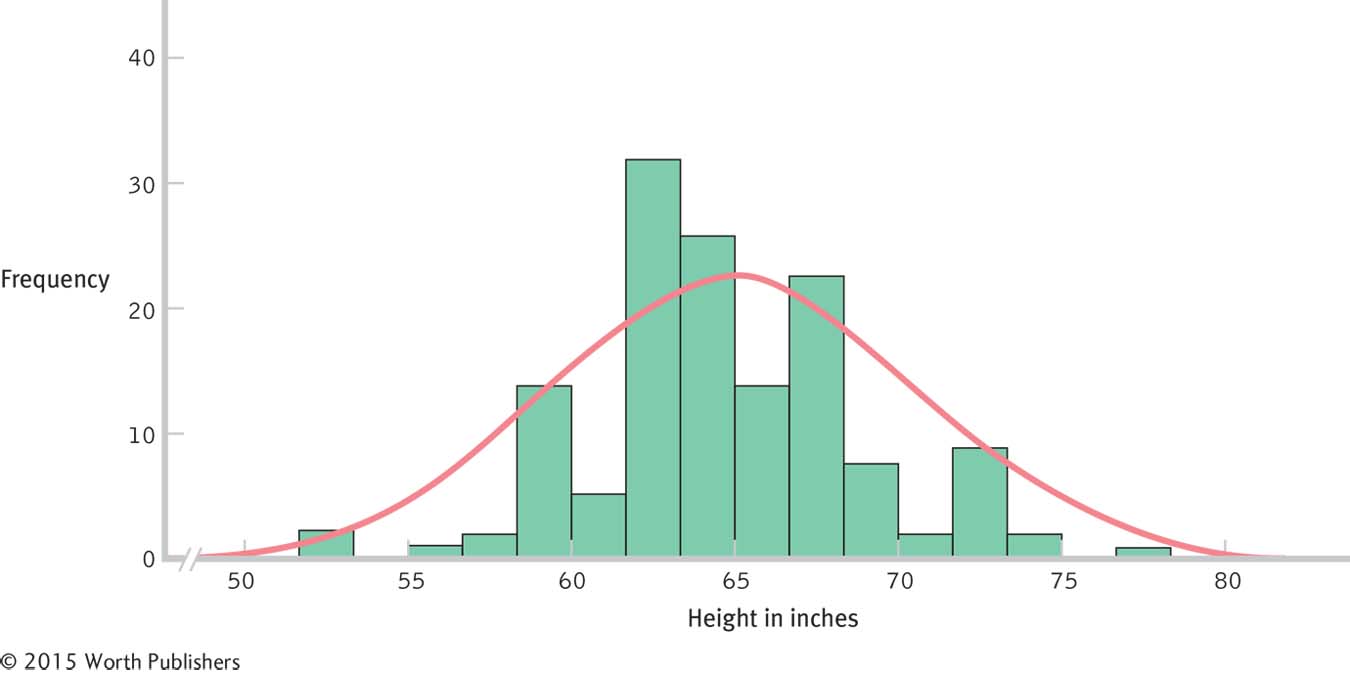
image
image
Figure 6.5: FIGURE 6-4
Sample of 140
Here is a histogram of the heights in inches of 140 students. As the sample increases, the shape of the distribution becomes more and more like the normal curve we would see for an entire population. Imagine the distribution of the data for a sample of 1000 students or of 1 million.

These three images demonstrate why sample size is so important in relation to the normal curve. As the sample size increases, the distribution more and more closely resembles a normal curve (as long as the underlying population distribution is normal). Imagine even larger samples—of 1000 students or of 1 million. As the size of the sample approaches the size of the population, the shape of the distribution tends to be normally distributed.

128

CHECK YOUR LEARNING

Reviewing the Concepts

  • The normal curve is a specific, mathematically defined curve that is bell-shaped, unimodal, and symmetric.

  • The normal curve describes the distributions of many variables.

  • As the size of a sample approaches the size of the population, the distribution resembles a normal curve (as long as the population is normally distributed).
Clarifying the Concepts 6-1 What does it mean to say that the normal curve is unimodal and symmetric?
Calculating the Statistics 6-2 A sample of 225 students completed the Consideration of Future Consequences (CFC) scale. The scores are means of responses to 12 items. Overall CFC scores range from 1 to 5.

  1. Here are CFC scores for 5 students, rounded to the nearest whole or half number: 3.5, 3.5, 3.0, 4.0, and 2.0. Create a histogram for these data, either by hand or by using software.

  2. Now create a histogram for these scores of 30 students:

    3.5 3.5 3.0 4.0 2.0 4.0 2.0 4.0 3.5 4.5
    4.5 4.0 3.5 2.5 3.5 3.5 4.0 3.0 3.0 2.5
    3.0 3.5 4.0 3.5 3.5 2.0 3.5 3.0 3.0 2.5
Applying the Concepts 6-3 The histogram below uses the actual (not rounded) CFC scores for all 225 students described in 6-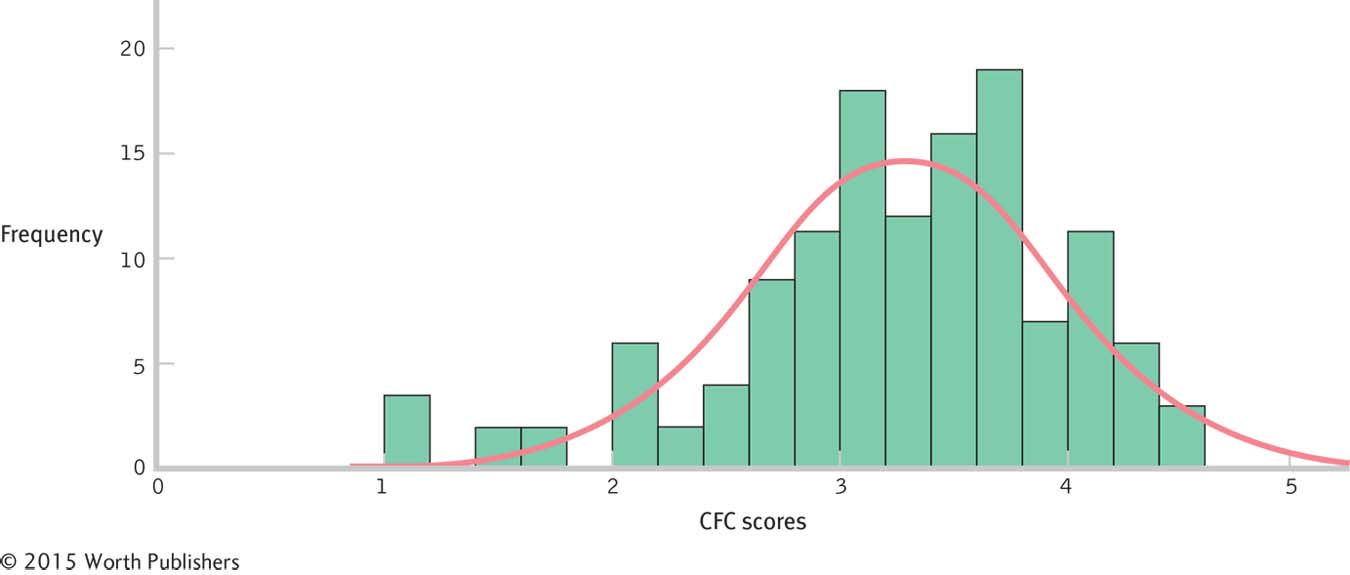2. What do you notice about the shape of this distribution of scores as the size of the sample increases?
image

Solutions to these Check Your Learning questions can be found in Appendix D.