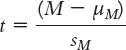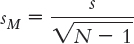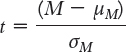When should we use a t distribution?

Why do we modify the formula for calculating standard deviation when using t tests (and divide by N − 1)?

How is the calculation of standard error different for a t test than for a z test?

Explain why the standard error for the distribution of sample means is smaller than the standard deviation of sample scores.

Define the symbols in the formula for the t statistic:

When is it appropriate to use a single-sample t test?

What does the phrase “free to vary,” referring to a number of scores in a given sample, mean for statisticians?

How are the critical t values affected by sample size and degrees of freedom?

Why do the t distributions merge with the z distribution as sample size increases?

Explain what each part of the following statistical phrase means, as it would be reported in APA format: t(4) = 2.87, p = 0.032.

What do we mean when we say we have a distribution of mean differences?

When do we use a paired-samples t test?

Explain the distinction between the terms independent samples and paired samples as they relate to t tests.

How is a paired-samples t test similar to a single-sample t test?

How is a paired-samples t test different from a single-sample t test?

Why is the population mean almost always equal to 0 for the null hypothesis in the two-tailed, paired-samples t test?

If we calculate the confidence interval around the sample mean difference used for a paired-samples t test, and it includes the value of 0, what can we conclude?

If we calculate the confidence interval around the sample mean difference used for a paired-samples t test, and it does not include the value of 0, what can we conclude?

Why is a confidence interval more useful than a single-sample t test or a paired-samples t test?

What is the appropriate effect size for a paired-samples t test? How is the calculation different from the effect size for a single-sample t test?

For a paired-samples t test, how is a Cohen’s d of 0.5 interpreted, according to Cohen’s conventions?

We use formulas to describe calculations. Find the error in each of the following formulas. Explain why each is incorrect and provide a correction.

For the data 93, 97, 91, 88, 103, 94, 97, calculate the standard deviation under both of these conditions:

For the data 1.01, 0.99, 1.12, 1.27, 0.82, 1.04, calculate the standard deviation under both of the following conditions. (Note: You will have to carry some calculations out to the third decimal place to see the difference in calculations.)

Identify the critical t value in each of the following circumstances:

Calculate degrees of freedom and identify the critical t value for a single-sample t test in each of the following circumstances:

Identify the critical t values for each of the following tests:

Assume we know the following for a two-tailed, single-sample t test, at a p level of 0.05: µ = 44.3, N = 114, M = 43, s = 5.9.

Assume we know the following for a two-tailed, single-sample t test: µ = 7, N = 41, M = 8.5, s = 2.1.

Using Cohen’s conventions, interpret the effect sizes that you calculated in:

Identify critical t values for each of the following tests:

Assume 8 participants completed a mood scale before and after watching a funny video clip.

The following are scores for 8 students on two different exams.

The following are mood scores for 12 participants before and after watching a funny video clip (higher values indicate better mood).

Consider the following data:

Consider the following data.

Assume we know the following for a paired-samples t test: N = 13, M_difference = −0.77, s = 1.42.

Assume we know the following for a paired-samples t test: N = 32, M_difference = 1.75, s = 4.0.

The relation between the z distribution and the t distributions: For the hypothesis tests described below in parts (a) through (c), one of which is the same as that described in Exercise 9.31a, identify what the critical z value would have been if there had been just one sample and we knew the mean and standard deviation of the population:

t statistics and standardized tests: On its Web site, the Princeton Review claims that students who have taken its course improve their Graduate Record Examination (GRE) scores, on average, by 210 points (based on the old scoring system). (No other information is provided about this statistic.) Treating this average gain as a population mean, a researcher wonders whether the far cheaper technique of practicing for the GRE on one’s own would lead to a different average gain. She randomly selects five students from the pool of students at her university who plan to take the GRE. The students take a practice test before and after 2 months of self-study. They reported (fictional) gains of 160, 240, 340, 70, and 250 points. (Note that many experts suggest that the results from self-study are similar to those from a structured course for students who have the self-discipline to study on their own. Regardless of the format, preparation has been convincingly demonstrated to lead to increased scores, on average.)

Single-sample t test, military training, and anger: Bardwell, Ensign, and Mills (2005) assessed the moods of 60 male U.S. Marines following a month-long training exercise conducted in cold temperatures and at high altitudes. Negative moods, including fatigue and anger, increased substantially during the training and lasted up to 3 months after the training ended. Mean mood scores were compared to population norms for three groups: college men, adult men, and male psychiatric outpatients. Let’s examine anger scores for six Marines at the end of training; these scores are fictional, but their mean and standard deviation are very close to the actual descriptive statistics for the sample: 14, 12, 13, 12, 14, 15.

t tests and the cost of Levi’s jeans and H&M dresses in Halifax: Numbeo is a crowd-sourced Web site that gathers data on cities and countries around the world (http://www.numbeo.com/cost-of-living/). Visitors to the site can add information on variables such as cost of living, traffic, and crime. The data are searchable by city or country. For example, when we looked up Halifax, Canada, we discovered that a pair of jeans (“Levis 501 or similar”) goes for an average of $62.50 (Numbeo, 2015). The range was $50 to $75. And a summer dress from somewhere like Zara or H&M goes for an average of $48, with a range of $40 to $60. Numbeo also tells us that their Halifax data are based on contributions from 80 different people.

242

Brain exercises and a paired-samples t test: PowerBrainRx, a Hong Kong-based for-profit company, promises to improve cognition. Their Web site lists testimonials, including one from a parent whose children “seemed to have better working memories, improved problem solving ability like mathematics, more logical thinking and better academic performance” following mental exercise training. There are numerous ads for companies like PowerBrainRx on the Internet and on late-night television, but there does not seem to be a lot of research examining the specific programs these companies are selling. How could you design a study for PowerBrainRx that would use a paired-samples t test to analyze the data?

t tests and retail: Many communities worldwide are lamenting the effects of so-called big box retailers (e.g., Walmart) on their local economies, particularly on small, independently owned shops. Do these large stores affect the bottom lines of locally owned retailers? Imagine that you decide to test this premise. You assess earnings at 20 local stores for the month of October, a few months before a big box store opens. You then assess earnings the following October, correcting for inflation.

Paired-samples t tests, confidence intervals, and hockey goals: Below are the numbers of goals scored by the lead scorers of the New Jersey Devils hockey team in the 2007–2008 and 2008–2009 seasons. On average, did the Devils play any differently in 2008–2009 than they did in 2007–2008?

Paired-samples t test and graduate admissions: Is it harder to get into graduate programs in psychology or in history? We randomly selected five institutions from among all U.S. institutions with graduate programs. The first number for each is the minimum grade point average (GPA) for applicants to the psychology doctoral program, and the second is for applicants to the history doctoral program. These GPAs were posted on the Web site of the well-known college guide company Peterson’s.

Attitudes toward statistics and the paired-samples t test: A professor wanted to know if her students’ attitudes toward statistics changed by the end of the course, so she asked them to fill out an “Attitudes Toward Statistics” scale at the beginning of the term and at the end of the term.

243

Paired-samples t tests, confidence intervals, and wedding-day weight loss: It seems that 14% of engaged women buy a wedding dress at least one size smaller than their current size. Why? Cornell researchers reported an alarming tendency for women who are engaged to sometimes attempt to lose an unhealthy amount of weight prior to their wedding (Neighbors & Sobal, 2008). The researchers found that engaged women weighed, on average, 152.1 pounds. The average ideal wedding weight reported by 227 women was 136.0 pounds. The data below represent the fictional weights of 8 women on the day they bought their wedding dress and on the day they got married. Did women lose weight for their wedding day?

Paired-samples t test, decorations in kindergarten classrooms, and science learning: Psychology researcher Anna Fisher and her colleagues studied whether kindergarten students learned better in decorated classrooms or undecorated classrooms, referred to as “sparse classrooms” (Fisher et al., 2014). They wondered whether students would be less distracted and learn better without decorations such as posters, maps, and children’s artwork. The same group of children had science lessons in a classroom without decorations and in a classroom with decorations. The students took a test on the material after each condition. Each child received a percentage-correct score, out of 100%, for each condition. In the journal article in which they reported their findings, the researchers wrote that the children’s “learning scores were higher in the sparse-classroom condition (M = 55%) than in the decorated-classroom condition (M = 42%), paired-samples t(22) = 2.95, p = .007; this effect was of medium size, Cohen’s d = 0.65.”

Paid days off and the single-sample t test: The number of paid days off (e.g., vacation, sick leave) taken by eight employees at a small local business is compared to the national average. You are hired as a consultant by the new business owner to help her determine how many paid days off she should provide. In general, she wants to set some standard for her employees and for herself. Let’s assume your search on the Internet for data on paid days off leaves you with the impression that the national average is 15 days. The data for the eight local employees during the last fiscal year are: 10, 11, 8, 14, 13, 12, 12, and 27 days.

Death row and the single-sample t test: The Florida Department of Corrections publishes an online death row fact sheet. It reports the average time on death row prior to execution as 11.72 years but provides no standard deviation. This mean is a parameter because it is calculated from the entire population of executed prisoners in Florida. Did the time spent on death row change over time? According to the execution list linked to the same Web site, the six prisoners executed in Florida during the years 2003, 2004, and 2005 spent 25.62, 13.09, 8.74, 17.63, 2.80, and 4.42 years on death row, respectively. (All were men, although Aileen Wuornos, the serial killer portrayed by Charlize Theron in the 2003 film Monster, was among the three prisoners executed by the state of Florida in 2002; Wuornos spent 10.69 years on death row.)

Political bias in academia and a paired-samples t test: The following is an excerpt from the abstract (brief opening summary) from a published research study that examined a reported bias against conservatives in American academia (Fosse, Gross, & Ma, 2011).

The American professoriate contains a disproportionate number of people with liberal political views. Is this because of political bias or discrimination?…We sent two emails to directors of graduate study in the leading American departments of sociology, political science, economics, history, and English. The emails came from fictitious students who expressed interest in doing graduate work in the department…. We analyze responses received in terms of frequency, timing, amount of information provided about the department, emotional warmth, and enthusiasm toward the student. (p. 1)

One of the fictional emails was from a fictional student who mentioned working on the presidential campaign of John McCain, a well-known conservative, and one was from a fictional student who mentioned working on the presidential campaign of Barack Obama, a well-known liberal. The researchers conducted a series of paired-samples t tests but did not find statistically significant differences on the various measures between ratings of the conservative and liberal students.

Hypnosis and the Stroop effect: In Chapter 1, you were given an opportunity to complete the Stroop test, in which color words are printed in the wrong color; for example, the word red might be printed in the color blue. The conflict that arises when we try to name the color of ink the words are printed in but are distracted when the color word does not match the ink color increases reaction time and decreases accuracy. Several researchers have suggested that the Stroop effect can be decreased by hypnosis. Raz, Fan, and Posner (2005) used brain-imaging techniques to demonstrate that posthypnotic suggestion led highly hypnotizable people to see Stroop words as nonsense words. Imagine that you are working with Raz and colleagues and your assignment is to determine whether reaction times decrease (remember, a decrease is a good thing; it indicates that participants are faster) when highly hypnotizable people receive a posthypnotic suggestion to view the words as nonsensical. You conduct the experiment on six participants, once in each condition, and receive the following data; the first number is reaction time in seconds without the posthypnotic suggestion, and the second number is reaction time with the posthypnotic suggestion:

245