Gene Interaction That Produces Novel Phenotypes
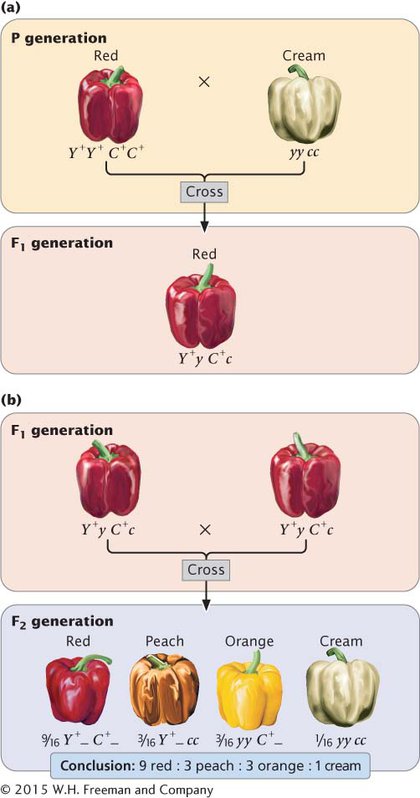
Let’s begin by examining gene interaction in which genes at two loci interact to produce a single characteristic. Fruit color in the pepper Capsicum annuum is determined in this way. Certain types of pepper plants produce fruits in one of four colors: red, peach, orange (sometimes called yellow), and cream (or white). If a homozygous plant with red peppers is crossed with a homozygous plant with cream peppers, all the F1 plants have red peppers (Figure 4.17a). When the F1 are crossed with each other, the F2 show a ratio of 9 red : 3 peach : 3 orange : 1 cream (Figure 4.17b). This dihybrid ratio (see Chapter 3) is produced by a cross between two plants that are both heterozygous for two loci (Y+y C+c × Y+y C+c). In this example, the Y locus and the C locus interact to produce a single phenotype—
| Genotype | Phenotype |
|---|---|
| Y+_ C+_ | red |
| Y+_ cc | peach |
| yy C+_ | orange |
| yy cc | cream |
To illustrate how Mendel’s rules of heredity can be used to understand the inheritance of characteristics determined by gene interaction, let’s consider a testcross between an F1 plant from the cross in Figure 4.17 (Y+y C+c) and a plant with cream peppers (yy cc). As outlined in Chapter 3 for independent loci, we can work this cross by breaking it down into two simple crosses. At the first locus, the heterozygote Y+y is crossed with the homozygote yy; this cross produces ½ Y+y and ½ yy progeny. Similarly, at the second locus, the heterozygous genotype C+c is crossed with the homozygous genotype cc, producing ½ C+c and ½ cc progeny. In accord with Mendel’s principle of independent assortment, these single-
| Progeny Genotype | Probability at each locus | Overall probability | Phenotype | |
|---|---|---|---|---|
| Y+y C+c | ½ × ½ | = | ¼ | red peppers |
| Y+y cc | ½ × ½ | = | ¼ | peach peppers |
| yy C+c | ½ × ½ | = | ¼ | orange peppers |
| Yy cc | ½ × ½ | = | ¼ | cream peppers |
When you work problems with gene interaction, it is especially important to determine the probabilities of single- TRY PROBLEM 33
TRY PROBLEM 33