CHAPTER 10 Review Exercises

526

Question 10.73

10.73 What’s wrong?

For each of the following, explain what is wrong and why.

  1. The slope describes the change in for a unit change in .
  2. The population regression line is .
  3. A 95% confidence interval for the mean response is the same width regardless of .

10.73

(a) and are reversed, the slope describes the change in for a unit change in . (b) The population regression line uses parameters, . (c) This is incorrect, the width of the interval widens the further from .

Question 10.74

10.74 What’s wrong?

For each of the following, explain what is wrong and why.

  1. The parameters of the simple linear regression model are , , and .
  2. To test , use a test.
  3. For any value of the explanatory variable , the confidence interval for the mean response will be wider than the prediction interval for a future observation.

Question 10.75

10.75 College debt versus adjusted in-state costs.

Kiplinger’s “Best Values in Public Colleges” provides a ranking of U.S. public colleges based on a combination of various measures of academics and affordability.19 We’ll consider a random collection of 40 colleges from Kiplinger’s 2014 report and focus on the average debt in dollars at graduation (AvgDebt) and the in-state cost per year after need-based aid (InCostAid).

bestval

  1. A scatterplot of these two variables is shown in Figure 10.20. Describe the relationship. Are there any possible outliers or unusual values? Does a linear relationship between InCostAid and AvgDebt seem reasonable?
  2. Based on the scatterplot, approximately how much does the average debt change for an additional $1000 of annual cost?
  3. Colorado School of Mines is a school with an adjusted in-state cost of $22,229. Discuss the appropriateness of using this data set to predict the average debt for this school.
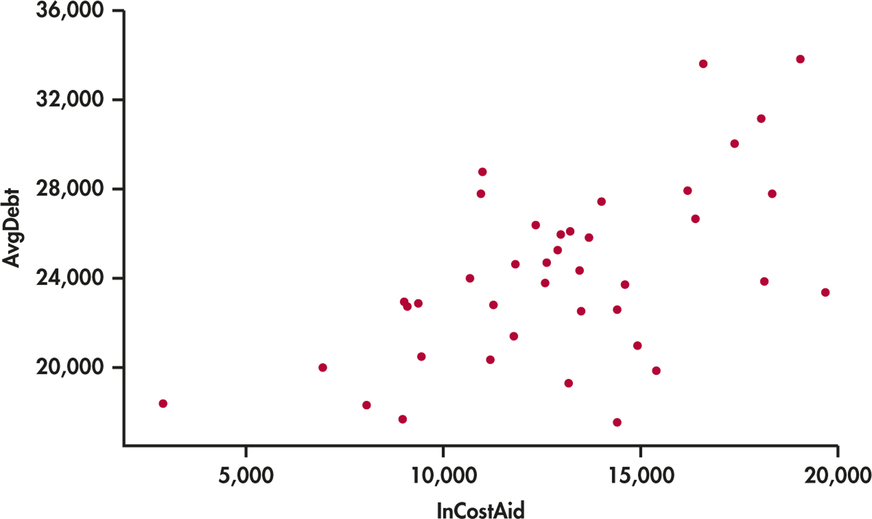
image
Figure 10.20: FIGURE 10.20 Scatterplot of average debt (in dollars) at graduation versus the in-state cost per year (in dollars) after need-based aid, Exercise 10.75.

10.75

(a) The data are weakly linear and positive. There is one college with a very low InCostAid value. A linear model seems appropriate. (b) Answers will vary because it is difficult to tell from the scatterplot. The actual value is around $650. (c) Because the Colorado School of Mines instate cost falls outside the range for our dataset, it would be extrapolation and likely yield an incorrect prediction.

Question 10.76

10.76 Can we consider this an SRS?

Refer to the previous exercise. The report states that Kiplinger’s rankings focus on traditional four-year public colleges with broad-based curricula. Each year, they start with more than 500 schools and then narrow the list down to roughly 120 based on academic quality before ranking them. The data set in the previous exercise is an SRS from their published list of 100 schools. As far as investigating the relationship between the average debt and the in-state cost after adjusting for need-based aid, is it reasonable to consider this to be an SRS from the population of interest? Write a short paragraph explaining your answer.

bestval

Question 10.77

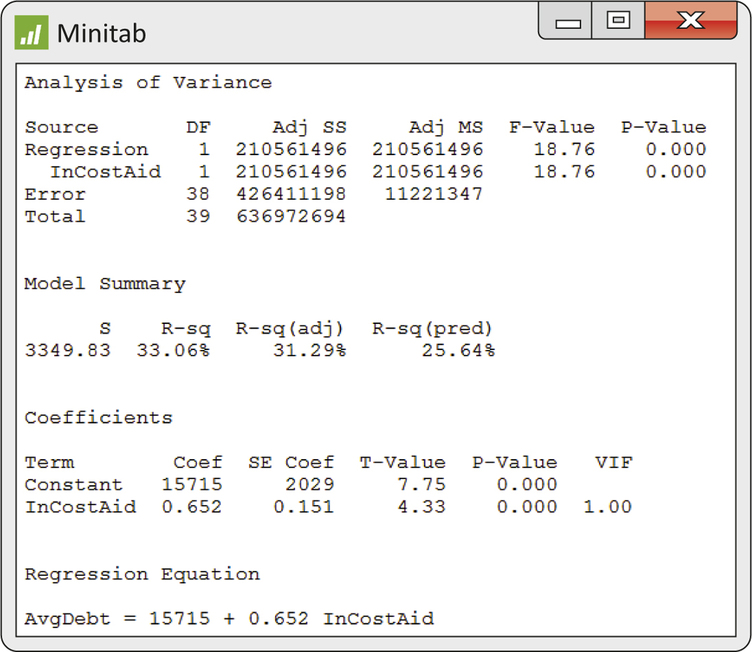
10.77 Predicting college debt.

Refer to Exercise 10.75. Figure 10.21 contains Minitab output for the simple linear regression of AvgDebt on InCostAid.

bestval

  1. State the least-squares regression line.
  2. The University of Oklahoma is one school in this sample. It has an in-state cost of $12,960 and average debt of $26,005. What is the residual?
  3. Construct a 95% confidence interval for the slope. What does this interval tell you about the change in average debt for a change in the in-state cost?

10.77

(a) . (b) . (c) The interval is (0.3473, 0.9567). For each $1000 of in-state cost, we expect on average an average debt of between $347 and $957 at graduation with 95% confidence.

Question 10.78

10.78 More on predicting college debt.

Refer to the previous exercise. The University of Minnesota has an in-state cost of $14,933 and an average debt of $29,702. Texas A&M University has an in-state cost of $9007 and an average debt of $22,955.

bestval

527

image
Figure 10.21: FIGURE 10.21 Minitab output for the regression of average debt (in dollars) at graduation on the in-state cost (in dollars) per year, Exercise 10.77.
  1. Using your answer to part (a) of the previous exercise, what is the predicted average debt for a student at the University of Minnesota?
  2. What is the predicted average debt for Texas A&M University?
  3. Without doing any calculations, would the standard error for the estimated average debt be larger for the University of Minnesota or the Texas A&M University? Explain your answer.

Question 10.79

10.79 Predicting college debt: Other measures.

Refer to Exercise 10.75. Let’s now look at AvgDebt and its relationship with all six measures available in the data set. In addition to the in-state cost after aid (InCostAid), we have the admittance rate (Admit), the four-year graduation rate (Grad), in-state cost before aid (InCost), out-of-state cost before aid (OutCost), and the out-of-state cost after aid (OutCostAid).

bestval

  1. Generate scatterplots of each explanatory variable and AvgDebt. Do all these relationships look linear? Describe what you see.
  2. Fit each of the explanatory variables separately and create a table that lists the explanatory variable, model standard deviation , and the -value for the test of a linear association.
  3. Which variable appears to be the best single explanatory variable of average debt? Explain your answer.

10.79

  1. Only InCostAid, Grad, and maybe InCost look linear.
  2. Variable -value
    InCostAid 3349.8 0.0001
    Admit 4092.0 0.8408
    Grad 3611.2 0.0021
    InCost 3797.0 0.0174
    OutCost 4056.1 0.4022
    OutCostAid 3977.8 0.1413
  3. InCostAid is the single best explanatory variable; it has the most significant -value and the smallest model standard deviation .

Question 10.80

10.80 Yearly number of tornadoes.

The Storm Prediction Center of the National Oceanic and Atmospheric Administration maintains a database of tornadoes, floods, and other weather phenomena. Table 10.6 summarizes the annual number of tornadoes in the United States between 1953 and 2013.20

twister

  1. Make a plot of the total number of tornadoes by year. Does a linear trend over years appear reasonable? Are there any outliers or unusual patterns? Explain your answer.
  2. Run the simple linear regression and summarize the results, making sure to construct a 95% confidence interval for the average annual increase in the number of tornadoes.
  3. Obtain the residuals and plot them versus year. Is there anything unusual in the plot?
  4. Are the residuals Normal? Justify your answer.
  5. The number of tornadoes in 2004 is much larger than expected under this linear model. Also, the number of tornadoes in 2012 is much smaller than predicted. Remove these observations and rerun the simple linear regression. Compare these results with the results in part (b). Do you think these two observations should be considered outliers and removed? Explain your answer.

528

Table 10.13: TABLE 10.6 Annual number of tornadoes in the United States between 1953 and 2013
Year Number of
tornadoes		 Year Number of
tornadoes		 Year Number of
tornadoes		 Year Number of
tornadoes
1953 421 1969 608 1985 684 2001 1215
1954 550 1970 653 1986 764 2002 934
1955 593 1971 888 1987 656 2003 1374
1956 504 1972 741 1988 702 2004 1817
1957 856 1973 1102 1989 856 2005 1265
1958 564 1974 947 1990 1133 2006 1103
1959 604 1975 920 1991 1132 2007 1096
1960 616 1976 835 1992 1298 2008 1692
1961 697 1977 852 1993 1176 2009 1156
1962 657 1978 788 1994 1082 2010 1282
1963 464 1979 852 1995 1235 2011 1691
1964 704 1980 866 1996 1173 2012 939
1965 906 1981 783 1997 1148 2013 908
1966 585 1982 1046 1998 1449
1967 926 1983 931 1999 1340
1968 660 1984 907 2000 1075

Question 10.81

10.81 Plot indicates model assumptions.

Construct a plot with data and a regression line that fits the simple linear regression model framework. Then construct another plot that has the same slope and intercept but a much smaller value of the regression standard error .

10.81

Answers will vary. The plot with smaller should have the data points closer to the line.

Question 10.82

10.82 Significance tests and confidence intervals.

The significance test for the slope in a simple linear regression gave a value with 28 degrees of freedom. Would the 95% confidence interval for the slope include the value zero? Give a reason for your answer.

Question 10.83

10.83 Predicting college debt: One last measure.

Refer to Exercises 10.75, 10.77, and 10.79. Given the in-state cost prior to and after aid, another measure is the average amount of need-based aid. Create this new variable by subtracting these two costs, and investigate its relationship with average debt. Write a short paragraph summarizing your findings.

bestval

10.83

The effect of need-based aid on average debt is negative; the estimated regression slope is −0.10137, indicating that for every $1000 of need-based aid, the average debt goes down by $101.37, but it is not significant. . There is no significant linear relationship between average debt and need-based aid.

Question 10.84

10.84 Brand equity and sales.

Brand equity is one of the most important assets of a business. It includes brand loyalty, brand awareness, perceived quality, and brand image. One study examined the relationship between brand equity and sales using simple linear regression analysis.21 The correlation between brand equity and sales was reported to be 0.757 with a significance level of 0.001.

  1. Explain in simple language the meaning of these results.
  2. The study examined quick-service restaurants in Korea and was based on 394 usable surveys from a total of 950 that were distributed to shoppers at a mall. Write a short narrative commenting on the design of the study and how well you think the results would apply to other settings.

Question 10.85

10.85 Hotel sizes and numbers of employees.

A human resources study of hotels collected data on the size, measured by number of rooms, and the number of employees for 14 hotels in Canada.22 Here are the data.

hotsize

Employees Rooms Employees Rooms
1200 1388 275 424
180 348 105 240
350 294 435 601
250 413 585 1590
415 346 560 380
139 353 166 297
121 191 228 108

529

  1. To what extent can the number of employees be predicted by the size of the hotel? Plot the data and summarize the relationship.
  2. Is this the type of relationship that you would expect to see before examining the data? Explain why or why not.
  3. Calculate the least-squares regression line and add it to the plot.
  4. Give the results of the significance test for the regression slope with your conclusion.
  5. Find a 95% confidence interval for the slope.

10.85

(a) The relationship is linear, positive, and strong.
(b) Yes, a bigger hotel requires more employees to take care of both the rooms and the guests, so we would expect a positive slope.
(c) .
(d) . There is a significant linear relationship between the number of employees and the number of rooms for hotels.
(e) (0.25259, 0.77459).

Question 10.86

10.86 How can we use the results?

Refer to the previous exercise.

  1. If one hotel had 100 more rooms than another, how many additional employees would you expect that hotel to have?
  2. Give a 95% confidence interval for your answer in part (a).
  3. The study collected these data from 14 hotels in Toronto. Discuss how well you think the results can be generalized to other hotels in Toronto, to hotels in Canada, and to hotels in other countries.

Question 10.87

10.87 Check the outliers.

The plot you generated in Exercise 10.85 has two observations that appear to be outliers.

  1. Identify these points on a plot of the data.
  2. Rerun the analysis with the other 12 hotels, and summarize the effect of the two possible outliers on the results that you gave in Exercise 10.85.

10.87

(a) They are very large hotels with more than 1000 rooms. (b) The analysis changes drastically. . The data are no longer significant at the 5% level with these outliers removed. The previous results likely are not valid as the significance seen was just due to these 2 outliers.

Question 10.88

10.88 Growth in grocery store size.

Here are data giving the median store size (in square feet) by year for grocery stores.23

grocery

Year Store size Year Store size Year Store size
1993 33.0 2000 44.6 2007 47.5
1994 35.1 2001 44.0 2008 46.8
1995 37.2 2002 44.0 2009 46.2
1996 38.6 2003 44.0 2010 46.0
1997 39.3 2004 45.6 2013 46.5
1998 40.5 2005 48.1
1999 44.8 2006 48.8
  1. Use a simple linear regression and a prediction interval to give an estimate, along with a measure of uncertainty, for the median grocery store size in 2011 and in 2012.
  2. Plot the data with the regression line. Based on what you see, do you think that the answer that you computed in part (a) is a good prediction? Explain why or why not.

Question 10.89

10.89 Agricultural productivity.

Few sectors of the economy have increased their productivity as rapidly as agriculture. Let’s describe this increase. Productivity is defined as output per unit input. “Total factor productivity” (TFP) takes all inputs (labor, capital, fuels, and so on) into account. The data set AGPROD contains TFP for the years 1948–2011.24 The TFP entries are index numbers. That is, they give each year’s TFP as a percent of the value for 1948.

agprod

  1. Plot TFP against year. It appears that around 1980 the rate of increase in TFP changed. How is this apparent from the plot? What was the nature of the change?
  2. Regress TFP on year using only the data for the years 1948–1980. Add the least-squares line to your scatterplot. The line makes the finding in part (a) clearer.
  3. Give a 95% confidence interval for the annual rate of change in TFP during the period 1948–1980.
  4. Regress TFP on year for the years 1981–2011. Add this line to your plot. Give a 95% confidence interval for the annual rate of improvement in TFP during these years.
  5. Write a brief report on trends in U.S. farm productivity since 1948, making use of your analysis in parts (a) to (d).

10.89

(a) The rise from 1948 from 1980 is fairly consistent then shifts and increases at a much faster rate from 1981 to 2011. (b) . (c) (1.55206, 1.78825). (d) (2.93208, 3.53961). (e) Overall, there has been rapid growth in agricultural productivity since 1948. But there was a significant shift in that productivity around 1980. Before that, the growth, on average, was between 155% and 179% each year; after 1980, the growth was between 293% and 353% each year. These results are at 95% confidence.

530