Information-Processing Theories

• SCENE: DAUGHTER AND FATHER IN THEIR YARD.
• A PLAYMATE RIDES IN ON A BIKE.
  
  • Child: Daddy, would you unlock the basement door?
  • Father: Why?
  • C: ’Cause I want to ride my bike.
  • F: Your bike is in the garage.
  • C: But my socks are in the dryer.

What reasoning could have produced this 5-year-old’s enigmatic comment, “But my socks are in the dryer”? David Klahr, an eminent information-processing theorist, formulated the following model of the thought process that led to it:

• Top goal: I want to ride my bike.
  
  •   Bias: I need shoes to ride comfortably.
  •   Fact: I’m barefoot.
•  Subgoal 1: Get my sneakers.
  
  •   Fact: The sneakers are in the yard.
  •   Fact: They’re uncomfortable on bare feet.
•  Subgoal 2: Get my socks.
  
  •   Fact: The sock drawer was empty this morning.
  •   Inference: The socks probably are in the dryer.
•  Subgoal 3: Get them from the dryer.
  
  •   Fact: The dryer is in the basement.
•  Subgoal 4: Go to the basement.
  
  •   Fact: It’s quicker to go through the yard entrance.
  •   Fact: The yard entrance is always locked.
•  Subgoal 5: Unlock the door to the basement.
  
  •   Fact: Daddies have the keys to everything.
•  Subgoal 6: Ask Daddy to unlock the door.

Klahr’s analysis of his daughter’s thinking illustrates two notable characteristics of information-processing theories.¹ One is the precise specification of the processes involved in children’s thinking. Klahr’s approach, for example, used task analysis—that is, the identification of goals the obstacles that prevent their immediate realization, the prior knowledge and information in the environment relevant to them, and the potential processing strategies for overcoming the obstacles and attaining the goals.

Such task analysis helps information-processing researchers understand and predict children’s behavior and allows them to rigorously test precise hypotheses regarding how development occurs. In some cases, it also allows them to formulate computer simulations, a type of mathematical model that expresses ideas about mental processes in particularly precise ways. For example, Simon and Klahr (1995) created computer simulations of the knowledge and mental processes that led young children to fail on conservation problems and of the somewhat different knowledge and mental processes that allowed older children to succeed on them.

A second distinctive feature of information-processing analysis is an emphasis on thinking as an activity that occurs over time. Often, a single simple behavior, such as the initial request of Klahr’s daughter that he open the basement door, reflects an extended sequence of rapid mental operations. Information-processing analyses identify what those mental operations are, the order in which they are executed, and how increasing speed and accuracy of mental operations lead to cognitive growth.

View of Children’s Nature

Information-processing theorists see children’s cognitive growth as occurring continuously, in small increments that occur at different times on different tasks. This depiction differs fundamentally from Piaget’s belief that children progress through qualitatively distinct, broadly applicable stages, separated only by brief transition periods.

The Child as a Limited-Capacity Processing System

In trying to understand differences in children’s thinking at various ages, some information-processing theorists draw comparisons between the information processing of computers and that of humans. A computer’s information processing is limited by its hardware and by its software. The hardware limitations relate to the computer’s memory capacity and its efficiency in executing basic operations. The software limitations relate to the strategies and information that are available for performing particular tasks. People’s thinking is limited by the same factors: memory capacity, speed of thought processes, and availability of useful strategies and knowledge. In the information-processing view, cognitive development arises from children’s gradually surmounting their processing limitations through (1) expansion of the amount of information they can process at one time, (2) increases in the speed with which they execute thought processes, and (3) acquisition of new strategies and knowledge.

The Child as Problem Solver

Also central to the view of human nature held by information-processing theories is the assumption that children are active problem solvers. As suggested by Klahr’s analysis of his daughter’s behavior, problem solving involves goals, perceived obstacles, and strategies or rules for overcoming the obstacles and attaining the goals. A description of a younger child’s problem solving reveals the same combination of goal, obstacle, and strategy:

In addition to illustrating the typical goal–obstacle–strategy sequence, this example highlights another basic tenet of information-processing approaches: children’s cognitive flexibility helps them pursue their goals. Even young children show great ingenuity in surmounting the obstacles imposed by their parents, the physical environment, and their own lack of knowledge.

Central Developmental Issues

Like all the theories described in this chapter, information-processing theories examine how nature and nurture work together to produce development. What makes information-processing theories unique is their emphasis on precise descriptions of how change occurs. The way in which information-processing theories address the issues of nature and nurture and how change occurs can be seen particularly clearly in their accounts of the development of memory and problem solving.

The Development of Memory

Memory is crucial to everything we do. The skills we use on everyday tasks, the language we employ when writing or speaking, the emotions we feel on a given occasion—all depend on our memory of past experiences and the knowledge acquired through them. Indeed, without memory of our experiences, we lose our very identity, a devastating syndrome that has been observed in patients with certain types of amnesia (Reed & Squire, 1998). Memory plays a role in all cognitive developmental theories, but it is especially central to information-processing theories. Most such theories distinguish among working memory, long-term memory, and executive functions.

Working memory Working memory involves actively attending to, gathering, maintaining, storing, and processing information. For example, if after reading a story about birds, a child were asked a question about it, the child would, through working memory, bring together relevant information from the story, inferences made from that information, and prior knowledge about birds, and would then process the information to construct a reasonable answer.

Working memory is limited in both its capacity (the amount of information that it can store) and in the length of time it can retain information without updating activities. For example, a child might be able to remember a sequence of five digits but not six, and might be able to remember them for 5 or 10 seconds without repeating them but not for a longer time. The exact capacity and duration vary with the task and the type of material being processed, but for a given task and type of material, both capacity and speed increase with age and relevant experience (Schneider, 2011).

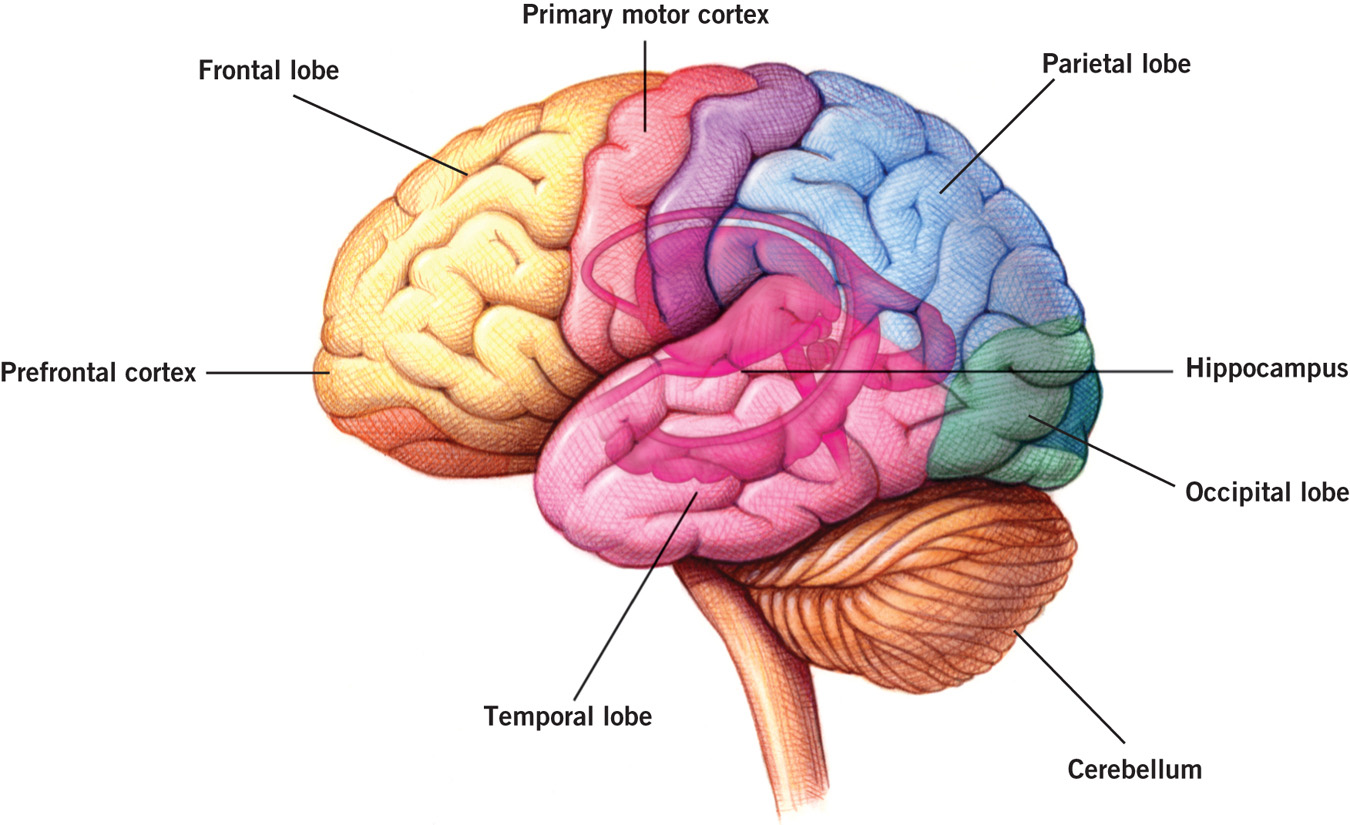
The basic organization of working-memory subsystems seems to be constant from early in childhood. However, the capacity and speed of operation of working memory increase greatly over the course of childhood and adolescence (Cowan et al., 1999; Gathercole et al., 2004). These changes are believed to occur in part because of increasing knowledge of the content on which working memory operates and in part because of maturational changes in the brain (Nelson, Thomas, & De Haan, 2013; see Figure 4.8).

FIGURE 4.8 All of the major areas of the cortex shown here continue maturing after birth. Brain maturation continues for a particularly long time in the prefrontal cortex, an area that is especially involved in planning, inhibiting inappropriate behavior, and adopting new goals in response to changing situations.

Long-term memory In contrast to the moment-to-moment nature of working memory, long-term memory consists of the knowledge that people accumulate over their lifetime. It includes factual knowledge (e.g., knowing the capitals of different countries or the teams that won the Super Bowl in the past 5 years), conceptual knowledge (e.g., the concepts of justice, mercy, and equality), procedural knowledge (e.g., knowing how to tie a shoe or play an Xbox game), attitudes (e.g., likes and dislikes regarding political parties or anchovies), reasoning strategies (e.g., knowing how to take an argument to its logical extreme to show its inadequacy), and so on. Long-term memory can thus be thought of as the totality of one’s knowledge, whereas working memory can be regarded as the subset of that knowledge that is being processed at a given time (Cowan, 2005; Ericsson & Kintsch, 1995).

In contrast to the severe limits on the capacity and duration of working memory, long-term memory can retain an unlimited amount of information for unlimited periods. To cite one notable example, research shows that people who studied Spanish or algebra in high school often retain a substantial amount of what they learned in the subject 50 years later, despite their not having used the information in the interim and their having accumulated vast stores of other skills, concepts, and knowledge in long-term memory over that period (Bahrick, 1987).

Executive Functioning Executive functions involve the control of cognition. The prefrontal cortex (Figure 4.8) plays a particularly important role in this cognitive control. Three major types of executive functions are inhibiting tempting actions that would be counterproductive; enhancing working memory through use of strategies, such as repeating a phone number that would otherwise be forgotten; and being cognitively flexible, for example, taking someone else’s perspective in an argument despite its differing from one’s own. As these examples suggest, executive functioning integrates information from working memory and long-term memory to accomplish goals (e.g., Diamond, 2013; Miyake & Friedman, 2012; Rose, Feldman, & Jankowski, 2011).

The ability of executive functions to control thinking and action—enabling the individual to respond appropriately rather than acting impulsively or doing what he or she is used to doing—increases greatly during the preschool and early elementary school years. One aspect of this improvement is children’s increased cognitive flexibility in shifting goals. For instance, when they are assigned the task of sorting toys by their color for a long period and then are asked to sort the same toys by shape, most 3-year-olds have difficulty switching goals, but 5-year-olds make the switch with ease (Baker, Friedman, & Leslie, 2010; Zelazo et al., 2003).

The ability to inhibit habitual responses occurs slightly later and is evident in everyday games such as “Simon Says.” Preschoolers have great difficulty inhibiting the impulse to quickly respond to commands that are not preceded by the critical phrase in such games, whereas early elementary school children are much better at inhibiting the impulse to act immediately (Dempster, 1995; Diamond, Kirkham, & Amso, 2002; Sabbagh et al., 2006). Strategies for controlling working memory tend to develop a little later, largely in the first few years of elementary school (Schneider, 2011).

As you might anticipate, the need for strong executive functioning continues to pose challenges well beyond early childhood. For example, resisting the temptation to daydream while doing one’s homework, keeping quiet while the teacher is talking, and inhibiting disrespectful replies to parents or teachers are difficult even for many adolescents (Bunge & Zelazo, 2006; Munakata, Snyder, & Chatham, 2011).

The quality of executive functioning during early childhood is highly predictive of many important life outcomes years later, including academic achievement in later grades, enrollment in college, and income and occupational status during adulthood (Blair & Razza, 2007; Duncan et al., 2007; McClelland & Cameron, 2011; Mischel & Ayduk, 2011; Moffitt et al., 2011). Fortunately, several training programs for preschoolers have shown considerable promise for improving young children’s executive functioning (Diamond et al., 2007, 2013; Raver et al., 2009).

In one such training study, disadvantaged preschoolers were randomly assigned to classrooms using a curriculum designed to improve executive functioning (Raver et al., 2011). The intervention involved instructing teachers in strategies—including stating and implementing clear rules, rewarding positive behaviors, and redirecting negative behaviors in positive directions—that would help children inhibit impulses to disrupt classroom activities. By the end of the school year, this approach had led to improvements in the children’s behavior and self-regulatory skills. Even more impressive, for the next 3 years, children who had been in the intervention classrooms continued to perform better in math and reading than did children in a control group (Raver et al., 2011).

Explanations of memory development Information-processing theorists try to explain both the processes that make memory as good as it is at each age and the limitations that prevent it from being better. These efforts have focused on three types of capabilities: basic processes, strategies, and content knowledge.

BASIC PROCESSES The simplest and most frequently used mental activities are known as basic processes. They include associating events with one another, recognizing objects as familiar, recalling facts and procedures, and generalizing from one instance to another. Another basic process, which is key to all the others, is encoding—the representation in memory of specific features of objects and events. With development, children execute basic processes more efficiently, enhancing their memory and learning for all kinds of materials.

Most of these basic processes are familiar, and their importance obvious. However, encoding is probably less familiar. Appreciating its significance requires some understanding of the way in which memory works. People often think of memory as something akin to an unedited video recording of our experiences. Actually, memory is far more selective. People encode information that draws their attention or that they consider relevant, but they fail to encode a great deal of other information. Information that is not encoded is not remembered later. This failure is probably evident in your own memory of the American flag; although you have seen it many times, you most likely have not encoded how the stars are arranged.

Misencoding common sayings can lead to memorable confusions.

1997 © BIL KEANE, INC. REPRINTED WITH SPECIAL PERMISSION OF KING F EATURE SYNDICATE

Studies of how children learn to solve balance-scale problems illustrate the importance of encoding for learning and memory. As discussed on page 139, most 5-year-olds predict that the side of the scale with more weight will go down, regardless of the distance of the weights from the fulcrum. Five-year-olds generally have difficulty learning more advanced approaches to solving balance-scale problems that take into account distance as well as weight, because they do not encode information about distance of the weights from the fulcrum. For example, 5-year-olds are shown a balance scale with varying arrangements of weights on pegs; the scale is then hidden behind a barrier, and the children are asked to reproduce the arrangement on an identical balance scale. Five-year-olds generally reproduce the correct number of weights on each side but rarely put them the correct distance from the fulcrum (Siegler, 1976). Teaching them to encode distance by telling them that both weight and distance are important enables them to learn more advanced balance-scale rules that peers who were not taught to encode distance have trouble learning (Siegler & Chen, 1998).

Like improved encoding, improved speed of processing plays a key role in the development of memory and learning. As shown in Figure 4.9, processing speed increases most rapidly at young ages but continues to increase in adolescence (Kail, 1991, 1997; Luna et al., 2004).

FIGURE 4.9 Increase with age in speed of processing on two tasks Note that the increase is rapid in the early years and more gradual later. (Data from Kail, 1991)

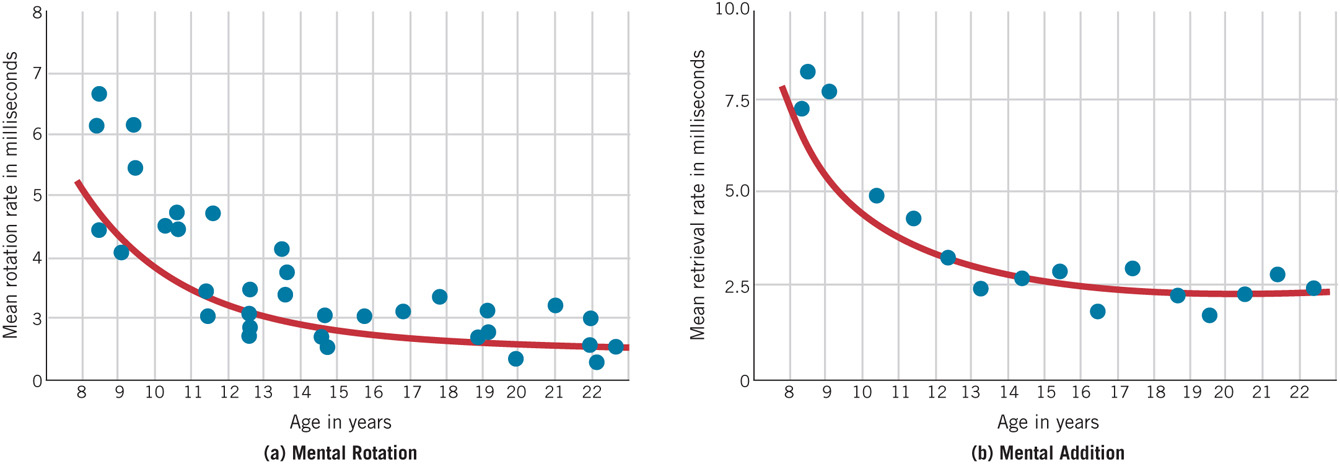
Two biological processes that contribute to faster processing are myelination and increased connectivity among brain regions (Luna et al., 2004). As discussed in Chapter 3, from the prenatal period through adolescence, increasing numbers of axons of neurons become covered with myelin, the fatty insulating substance that promotes faster and more reliable transmission of electrical impulses in the brain (Paus, 2009). Myelination enhances executive function, contributing to the ability to resist distractions (Dempster & Corkill, 1999; Wilson & Kipp, 1998). Greater connectivity among brain regions also increases processing capacity and speed by increasing the efficiency of communication among brain areas (Thatcher, 1998). This growth of long-distance connectivity among brain regions is especially prominent in later childhood and adolescence.

STRATEGIES Information-processing theories point to the acquisition and growth of strategies as another major source of the development of memory. Between ages 5 and 8 years, children begin to use a number of broadly useful memory strategies, among them the strategy of rehearsal, the repeating of information multiple times in order to remember it. The following newspaper item illustrates the usefulness of rehearsal for remembering information verbatim:

Had the boys witnessed the same event when they were 5-year-olds, they probably would not have rehearsed the numbers and would have forgotten the license number before the police arrived.

Another widely used memory strategy that becomes increasingly prevalent in the early elementary school years is selective attention, the process of intentionally focusing on the information that is most relevant to the current goal. If 7- and 8-year-olds are shown objects from two different categories (e.g., several toy animals and several household items) and are told that they later will need to remember the objects in only one category (e.g., “You’ll need to remember the animals”), they focus their attention on the objects in the specified category and remember more of them. In contrast, given the same instructions, 4-year-olds pay roughly equal attention to the objects in both categories, which reduces their memory for the objects they need to remember (DeMarie-Dreblow & Miller, 1988).

Through repeated visits to doctors’ offices and through other experiences that occur in more or less fixed sequences, children gain content knowledge that improves their memory for subsequent, similar events.

JLP/JOSE L. PELAEZ/CORBIS

CONTENT KNOWLEDGE With age and experience, children’s knowledge about almost everything increases. This increase in knowledge in long-term memory improves recall of new material by making it easier to integrate new material with existing understanding (Pressley & Hilden, 2006). The importance of content knowledge to memory is illustrated by the fact that when children know more about a topic than adults do, their memory for new information about the topic often is superior to the adults’. For example, when children and adults are provided new information about children’s TV programs and books, the children generally remember more of the information than do the adults (Lindberg, 1980, 1991). Similarly, children who know a lot about soccer learn more from reading new soccer stories than do other children who are both older and have higher IQs but who know less about soccer (Schneider, Körkel, & Weinert, 1989).

Prior content knowledge improves memory for new information in several different ways. One is by improving encoding. In tests of memory of various arrangements of chess pieces on a board, child chess experts remember far more than do adult novices. The reason is that the child experts’ greater knowledge of chess leads to their encoding higher-level chunks of information that include the positions of several pieces relative to one another rather than encoding the location of each piece separately (Chi & Ceci, 1987). Content knowledge also improves memory by providing useful associations. A child who is knowledgeable about birds knows that type of beak and type of diet are associated, so remembering either one increases memory for the other (Johnson & Mervis, 1994). In addition, content knowledge indicates what is and is not possible and therefore guides memory in useful directions. For example, when people familiar with baseball are asked to recall a particular inning of a game that they watched and they can remember only two outs in that inning, they recognize that there must have been a third out and search their memories for it; people who lack baseball knowledge do not (Spilich et al., 1979).

The Development of Problem Solving

As noted earlier, information-processing theories depict children as active problem solvers whose use of strategies often allows them to overcome limitations of knowledge and processing capacity. In this section, we present an information-processing perspective on the development of problem solving—the overlapping-waves theory. Piaget’s theory depicted children of a given age as using a particular strategy to solve a particular class of problems. For example, he described 5-year-olds as “solving” conservation-of-number problems (see Figure 4.6) by choosing the longer row of objects, and 7-year-olds as solving the same problems by reasoning that if nothing was added or subtracted, the number of objects must remain the same. According to overlapping-waves theory, however, children actually use a variety of approaches to solve this and other problems (Siegler, 1996). For instance, examining 5-year-olds’ reasoning on repeated trials of the conservation-of-number problem reveals that most children use at least three different strategies (Siegler, 1995). The same child who on one trial incorrectly reasons that the longer row must have more objects will on other trials correctly reason that just spreading a row does not change the number of objects, and on yet other trials will count the number of objects in the two rows to see which has more.

Figure 4.10 presents the typical pattern of development envisioned by the overlapping-waves approach, with strategy 1 representing the simplest strategy, and strategy 5, the most advanced. At the youngest age depicted, children usually use strategy 1, but they sometimes use strategy 2 or 4. With age and experience, the strategies that produce more successful performances become more prevalent; new strategies also are generated and, if they are more effective than previous approaches, are used increasingly. Thus, by the middle of the age range in Figure 4.10, children have added strategies 3 and 5 to the original group and have almost stopped using strategy 1.

FIGURE 4.10 The overlapping-waves model The overlapping-waves model proposes that, at any one age, children use multiple strategies; that with age and experience, they rely increasingly on more advanced strategies (the ones with the higher numbers); and that development involves changes in use of existing strategies as well as discovery of new approaches.

Young children’s overoptimism sometimes leads them to engage in dangerous activities. This particular plan worked out fine, but not all do.

PHOTOS COURTESY OF JODIE PLUMERT

This model has been shown to accurately characterize children’s problem solving in a wide range of contexts, including arithmetic, time-telling, reading, spelling, scientific experimentation, biological understanding, tool use, and recall from memory (Chen & Siegler, 2000; Kuhn & Franklin, 2006; Lee & Karmiloff-Smith, 2002; Miller & Coyle, 1999).

The overlapping-waves approach specifies several ways in which problem solving improves over the course of development. Children discover new strategies that are more effective than their previous ones, they learn to execute both new and old strategies more efficiently, and they choose strategies that are more appropriate to the particular situation (Miller & Coyle, 1999; Siegler, 2006).

All these sources of cognitive growth are evident in learning addition. During kindergarten and the first few years of elementary school, children’s knowledge of single-digit addition improves greatly. One reason is that children discover new strategies, such as counting-on (e.g., solving 2 + 9 by thinking “9, 10, 11”). Another source of improvement is faster and more accurate execution of all the strategies that children know (e.g., retrieval of answers from memory, counting from one, and counting-on). A third source of improvement is that children choose among strategies increasingly adaptively (e.g., using counting-on most often on problems with a large difference between the addends, such as 2 + 9, and counting from one on problems such as 7 + 8, which are difficult for them to solve correctly by using the other strategies they know (Geary, 2006; Siegler, 1987; Sieger & Jenkins, 1989). (Box 4.2 illustrates how information-processing analyses can improve education.)

Planning Problem solving is often more successful if people plan before acting. Children benefit from planning how to get to friends’ houses, how to get their way with parents, and how to break bad news to others in ways that are least likely to trigger angry reactions (Hudson, Sosa, & Schapiro, 1997). Despite the advantages of planning, however, children, and even adolescents, often fail to plan in situations in which it would help their problem solving (Berg et al., 1997). The question is why.

Information-processing analyses suggest that one reason planning is difficult for children is that it requires inhibiting the desire to solve the problem immediately in favor of first trying to construct the best strategy. Starting to work on an assigned paper without planning what will be written in the paper is one familiar example.

A second reason planning is difficult for young children is that they tend to be overly optimistic about their abilities and think that they can solve problems more effectively than their capabilities actually allow (Bjorklund, 1997; Schneider, 1998). This overconfidence can lead them to not plan, because they think they will succeed without doing so. Such overoptimism can lead young children to act rashly. For instance, 6-year-olds who overestimate their physical abilities have more accidents than do peers who evaluate their abilities more realistically, presumably because their confidence leads them not to plan how to avoid potential dangers (Plumert, 1995).

Over time, maturation of the prefrontal cortex, a part of the brain that is especially important for planning, along with experiences that reduce overoptimism or demonstrate the value of planning, lead to increases in the frequency and quality of planning, which improves problem solving (Chalmers & Lawrence, 1993). The improvements in the planning process take a long time, however; even 12-year-olds leave less distance between themselves and oncoming vehicles than adults do (Plumert, Kearney, & Cremer, 2004).

Box 4.2: applications: Educational Applications of Information-Processing Theories

Children’s knowledge of numbers when they begin kindergarten predicts their mathematics achievement years later—in elementary school, middle school, and even high school (Duncan et al., 2007; Stevenson & Newman, 1986). It is especially unfortunate, then, that kindergartners from low-income families lag far behind middle-income peers in counting, number recognition, arithmetic, and knowledge of numerical magnitudes (e.g., understanding that 7 is less than 9 and that both are closer to 10 than to 0 on a number line).

Playing this number board game improves preschoolers’ numerical knowledge.

ROBERT SIEGLER

What might account for these early differences in numerical knowledge of children from different economic backgrounds? An information-processing analysis suggested that experience playing numerical board games such as Chutes and Ladders might be important. In Chutes and Ladders, players must move a token across 100 consecutively numbered squares, advancing on each of their turns by the number of spaces determined by a spinner. The higher the number of the square on which a child’s token rests at any given point in the game, the greater the number of number names the child will have spoken and heard, the greater the distance the child will have moved the token from the first square, the greater the time the child will have been playing the game, and the greater the number of discrete hand movements with the token the child will have made. These verbal, spatial, temporal, and kinesthetic cues provide a broadly based, multisensory foundation for knowledge of numerical magnitudes, a type of knowledge that is closely related to mathematics achievement test scores (Booth & Siegler, 2006, 2008; Geary, 2011).

Ramani and Siegler (2008) applied this information-processing analysis to improving the numerical understanding of low-income preschoolers. The researchers randomly assigned 4- and 5-year-olds from low-income families to either an experimental number-board condition or a control color-board condition. The number-board condition was virtually identical to the first row of the Chutes and Ladders board; it included 10 squares numbered consecutively from left to right. On each turn, the child spun a dial that yielded a “1” or a “2” and moved his or her token the corresponding number of squares on the board, stating the number on each square in the process. For example, if a player’s token was on the square with the “4,” and the player spun a “2,” the player would say, “5, 6” while moving the token from the “4” to the “6.” Children in the color-board condition played the same game, except that their board had no numbers and the players would say the name of the color of each square as they advanced their token. Children in both conditions were given a pretest that examined their knowledge of numbers before playing the game, and then played the game for four 15-minute sessions over a 2-week period. At the end of the fourth session, the children were given a posttest on their knowledge of numbers; 9 weeks later, they were given a follow-up test identical to the pretest and posttest.

On the posttest, children who played the number board game showed improved knowledge of the numbers 1 through 10 on all four tasks that were presented—counting, reading of numbers, magnitude comparisons (e.g., “Which is bigger, 8 or 3?”), and estimates of the locations of numbers on a number line. Significantly, all the gains were maintained on the follow-up test 9 weeks later. In contrast, children who played the color board game showed no improvement in any aspect of number knowledge. Moreover, children’s reports of how often they played Chutes and Ladders and other board games at home was positively correlated with their initial knowledge on all four numerical tasks, and middle-income children reported playing numerical board games (though not video games) much more often than children from low-income backgrounds.

Subsequent studies demonstrated that playing the 1–10 board game also improves preschoolers’ ability to learn the answers to arithmetic problems, such as that 2 + 4 = 6 (Siegler & Ramani, 2009). Taken together, the evidence suggests that numerical board games represent a quick, effective, and inexpensive means of improving the numerical knowledge of low-income children before they start school.