10-3 A star’s distance can be determined by comparing its luminosity and brightness

Apparent brightness is a measure of how faint a star looks to us, whereas absolute magnitude is a measure of the star’s total light output. In addition to absolute magnitude, astronomers have formulated another way to judge the energy output of stars—by comparing how much energy stars emit compared to how much energy the Sun emits. The total amount of energy per second a star emits is called its luminosity. As we saw in Chapter 9, the Sun emits about 3.86 × 10²⁶ W (1 watt, or 1 W, is 1 joule per second) and is written as L_⊙. Most stars are less luminous than the Sun, but some blaze forth with a million times the Sun’s luminosity. For example, a star that emits 5 times more energy per second than our Sun does has a luminosity of 5 L_⊙. Knowing a star’s luminosity is essential for determining the star’s history, present-day internal structure, and future evolution.

Luminosity and the Inverse-Square Law

Go to Video 10-3

To determine the luminosity of a star, we first note that as light energy moves away from its source, it spreads out over increasingly larger regions of space. Imagine a sphere of radius d centered on the light source, as in Figure 10-6a. The amount of energy that passes each second through a square meter of the sphere’s surface area is the total luminosity of the source (L) divided by the total surface area of the sphere (equal to 4πd²). This quantity is usually known as the apparent brightness of the light (b), because how bright a light source appears depends on how much light energy per second enters through the area of a light detector (such as your eye). Apparent brightness is measured in watts per square meter (W/m²). In other words, there is a relationship between how bright something appears and how close it is—the closer a luminous object is, the brighter it appears, as illustrated in Figure 10-6b. Moreover, this relationship depends not just on the precise distance, but actually on the square of the distance. Written in the form of an equation, the relationship between apparent brightness and luminosity is

Inverse-square law relating apparent brightness and luminosity

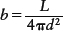
b = apparent brightness of a star’s light, in W/m²

L = star’s luminosity, in watts

d = distance to star, in meters

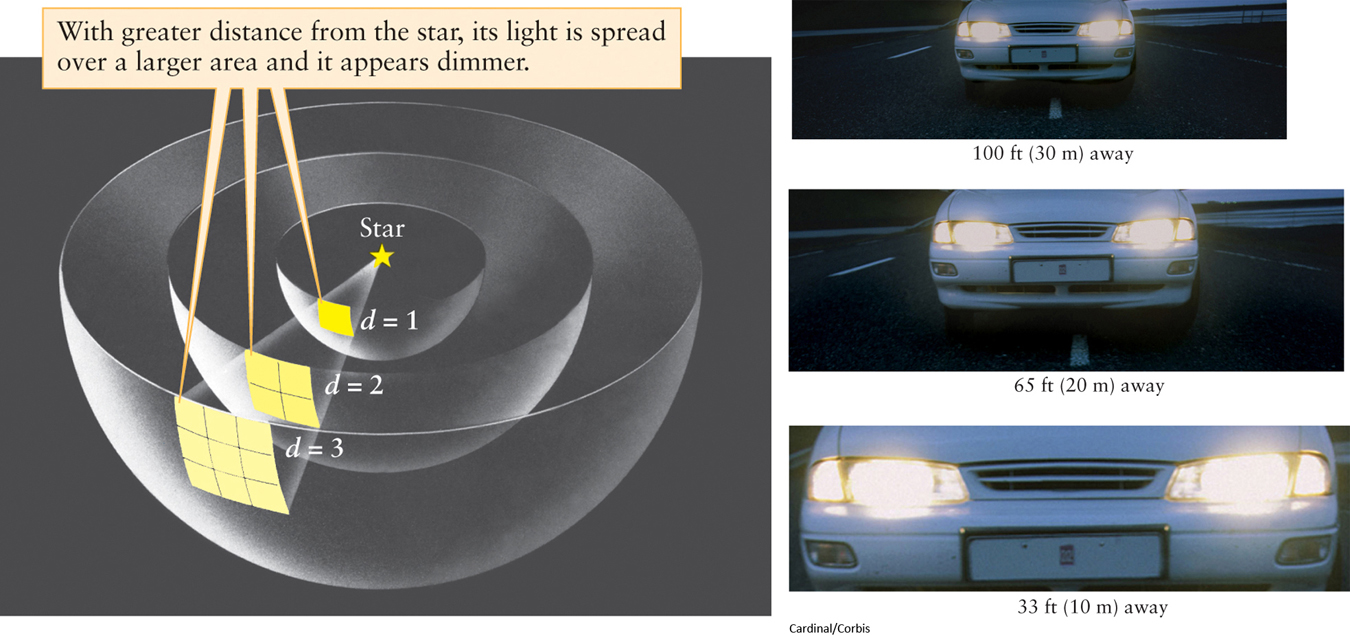
This relationship is called the inverse-square law, because the apparent brightness of light that an observer can see or measure is inversely proportional to the square of the observer’s distance (d) from the source. This mathematical equation might look complicated at first glance, but it is not. This equation says simply, if you double your distance from a lightbulb, its light is spread out over an area 4 times larger, so the apparent brightness you see is decreased by a factor of 4. Similarly, at triple the distance, the apparent brightness is one-ninth as great (see Figure 10-6a). For example, if we apply the inverse-square law to the Sun, which is 1.50 × 10¹¹ m from Earth, we can calculate the apparent brightness (b_⊙) as

Figure 10-6: The Inverse-Square Law (a) Energy from a light source illuminates an area that increases as the square of the distance from the source. Hence, the apparent brightness decreases as the square of the distance. The brightness at d = 2 is 1/(2²) = ¼ of the brightness at d = 1, and the brightness at d = 3 is 1/(3²) = % of that at d = 1. (b) The change in apparent brightness for a light source with constant luminosity as a result of changing distance is shown using an approaching automobile with headlights.

Another way of saying this is that a blanket spread out on the ground covering an area of 1 m² receives 1370 W of power from the Sun.

Astronomers measure the apparent brightness of a star using a telescope with an attached light-sensitive instrument, similar to the light meter in a camera that determines the proper exposure.

Calculating a Star’s Luminosity

The relationship between the apparent brightness of a shining star and its distance also allows astronomers to calculate the energy output of a star. This is important because a star’s appearance is dependent on both how far away it is and how much energy it is actually emitting. As it turns out, we need to know just two things to find a star’s luminosity: the distance to a star as compared to the Earth-Sun distance (the ratio d/d_⊙), and how that star’s apparent brightness compares to the brightness of the Sun (the ratio b/b_⊙). This important relationship can be written as a series of ratios as follows:

Determining a star’s luminosity from its apparent brightness

In other words, this mathematical relationship gives us a powerful rule relating the luminosity, distance, and apparent brightness of a star. For a specific apparent brightness, the more distant the star, the more luminous it must be to be seen from that distance.

As stars go, our Sun is neither extremely luminous nor extremely dim; it is a rather ordinary, garden-variety star. It is somewhat more luminous than most stars, however. Of the 30 closest stars to the Sun only 3 (α Centauri, Sirius, and Procyon) have a greater luminosity than the Sun.

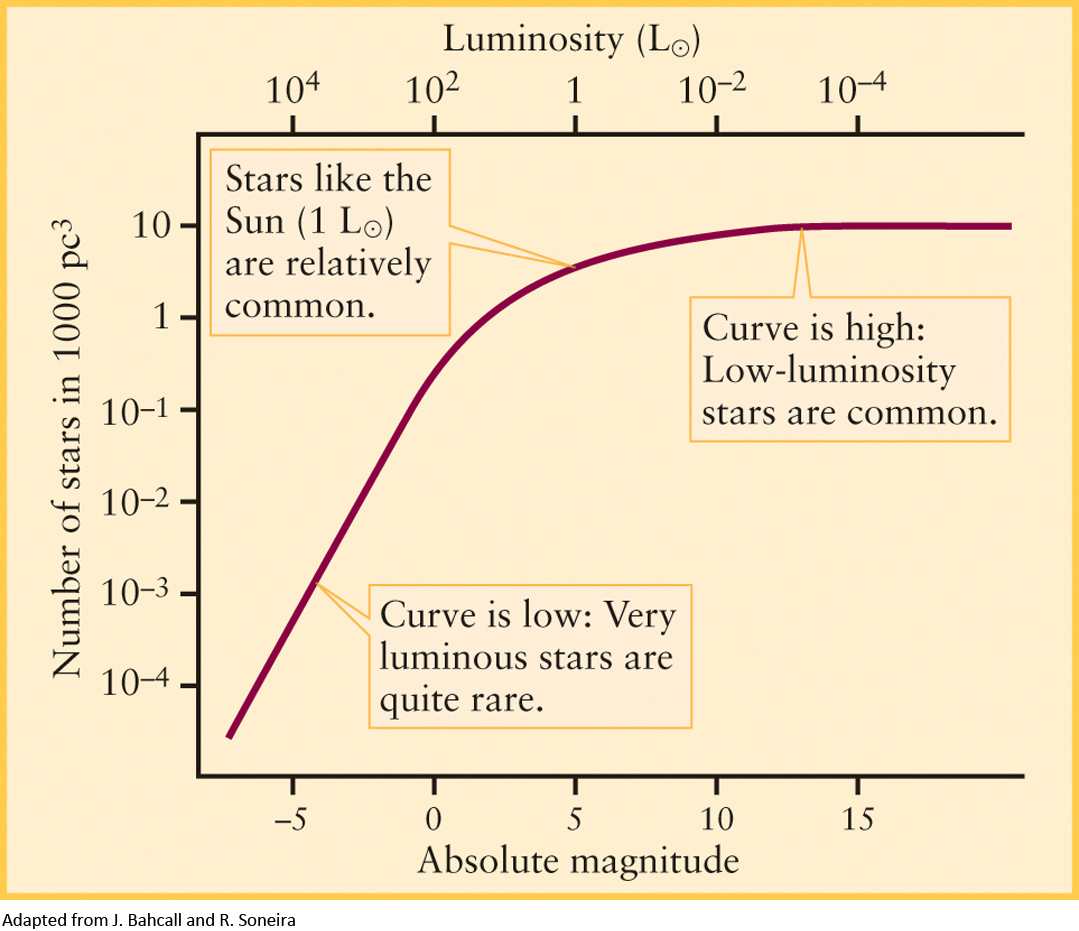
To better characterize a typical population of stars, astronomers count the stars out to a certain distance from the Sun and plot the number of stars that have different luminosities. Figure 10-7 shows the distribution of luminosities for stars in our part of the Milky Way Galaxy. The curve declines very steeply for the most luminous stars toward the left side of the graph, indicating that they are quite rare. For example, this graph shows that stars like the Sun are about 10,000 times more common than stars like Spica (which has a luminosity of 2100 L_⊙). The exact shape of the curve in Figure 10-7 applies only to the vicinity of the Sun and similar regions in our Milky Way Galaxy, with other locations having slightly different shaped curves.

Figure 10-7: The Luminosity Function This graph shows how many stars of a given luminosity lie within a nearby representative volume of 1000 pc³. The scale at the bottom of the graph shows absolute magnitude, an alternative measure of a star’s luminosity (described in Section 10-2).