10-7 Hertzsprung-Russell (H-R) diagrams reveal the different kinds of stars
Astronomers have collected a wealth of data about the stars, but merely having tables of numerical data is not enough. Like all scientists, astronomers want to analyze their data to look for trends and underlying principles. One of the best ways to look for trends in any set of data, whether it comes from astronomy, finance, medicine, or meteorology, is to create a graph showing how one quantity depends on another. For example, investors consult graphs of stock market values versus dates, and weather forecasters make graphs of temperature versus altitude to determine whether thunderstorms will form. Astronomers have found that a particular graph of stellar properties shows that stars fall naturally into just a few categories. This graph, one of the most important in all astronomy, will help us understand how stars form, evolve, and eventually die.
H-R Diagrams
 Go to Video 10-5
Go to Video 10-5
Which properties of stars should we include in a graph? Most stars have about the same chemical composition, but two properties of stars—their luminosities and surface temperatures—differ substantially from one star to another. What do we learn when we graph the luminosities of stars versus their surface temperatures?
One step toward answering this question was given in 1911 by the Danish astronomer Ejnar Hertzsprung. He pointed out that a regular pattern appears when the absolute magnitudes of stars (which measure their luminosities) are plotted against their colors (which measure their surface temperatures). Two years later, the American astronomer Henry Norris Russell independently discovered a similar regularity in a graph using spectral types (another measure of surface temperature) instead of colors. In recognition of their originators, graphs of this kind are today known as Hertzsprung-Russell diagrams, or H-R diagrams (Figure 10-15).
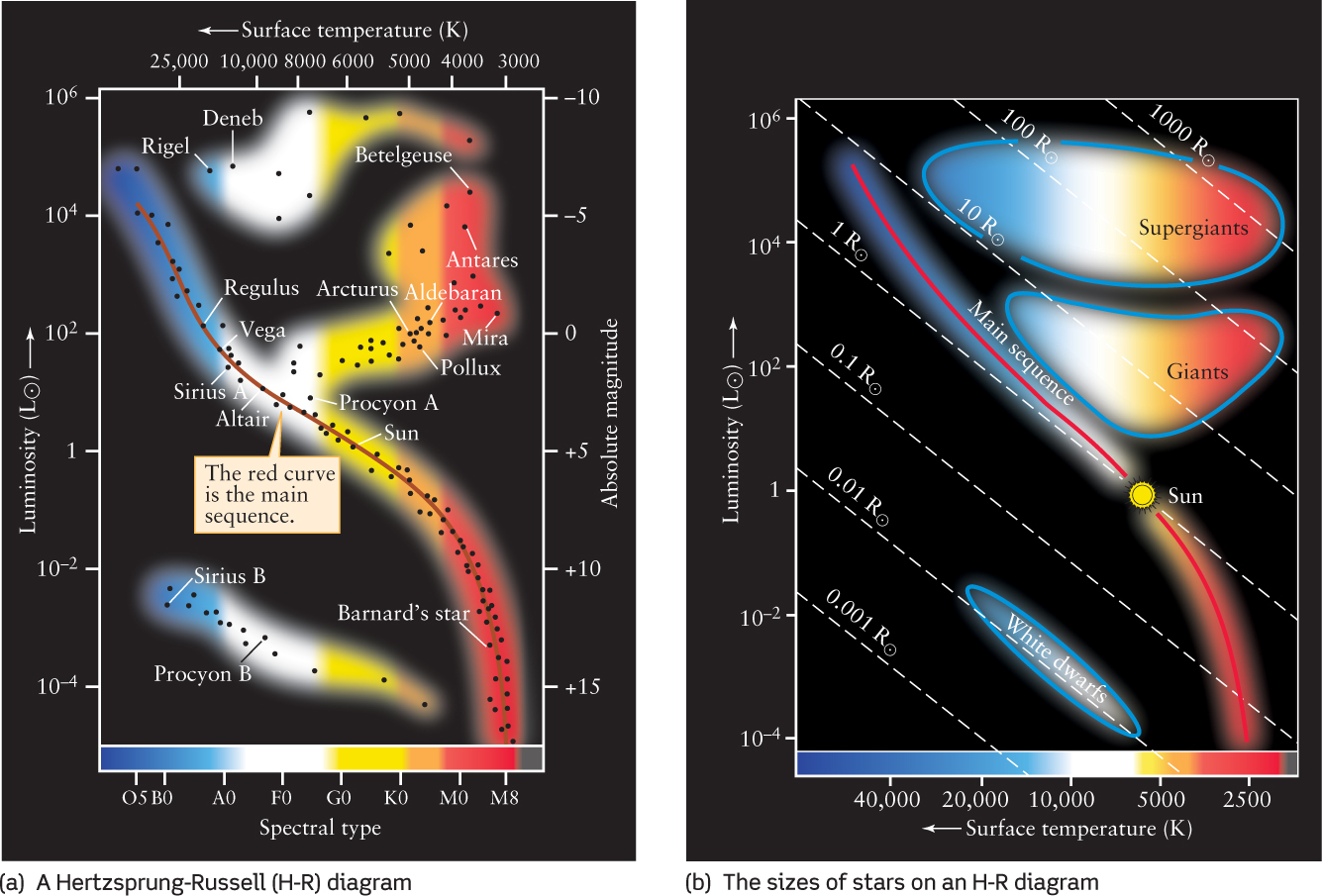
Figure 10-15a is a typical Hertzsprung-Russell diagram and it is a powerful tool for organizing the many characteristics of stars. Each dot represents a single star whose spectral type and luminosity have been determined. The most luminous stars are near the top of the diagram, the least luminous stars near the bottom. Hot stars of spectral classes O and B are toward the left side of the graph and cool stars of spectral class M are toward the right. The Sun is near the center of the various ranges.
CAUTION
You are probably accustomed to graphs in which the numbers on the horizontal axis increase as you move to the right. (For example, the business section of a newspaper includes a graph of stock market values versus dates, with later dates to the right of earlier ones.) But on an H-R diagram the temperature scale on the horizontal axis increases toward the left. This practice stems from the original diagrams of Hertzsprung and Russell, who placed hot O stars on the left and cool M stars on the right. This arrangement is a tradition that no one has seriously tried to change.
The most striking feature of the H-R diagram is that the data points are not scattered randomly over the graph but are grouped in a few distinct regions. The luminosities and surface temperatures of stars do not have random values; instead, these two quantities are related! The band stretching diagonally across the H-R diagram includes about 90% of the stars in the night sky. This band, called the main sequence, extends from the hot, luminous, blue stars in the upper left corner of the diagram to the cool, dim, red stars in the lower right corner. A star whose properties place it in this region of an H-R diagram is called a main-sequence star. The Sun (spectral type G2, luminosity 1 L⊙, absolute magnitude +4.8) is such a star. We will find that all main-sequence stars are like the Sun in that hydrogen fusion—thermonuclear reactions that convert hydrogen into helium—is taking place in their cores.
243
The upper right side of the H-R diagram shows a second major grouping of data points. Stars represented by these points are both luminous and cool. From the Stefan-Boltzmann law, we know that a cool star radiates much less light per unit of surface area than a hot star. In order for these stars to be as luminous as they are, they must be huge, and so they are called giants. These stars are around 10 to 100 times larger than the Sun. You can see this in Figure 10-15b, which is an H-R diagram to which dashed lines have been added to represent stellar radii. Most giant stars are around 100 to 1000 times more luminous than the Sun and have surface temperatures less than that of the Sun—only about 3000 K to 6000 K. Cooler members of this class of stars (those with surface temperatures from about 3000 K to 4000 K) are often called red giants because they appear reddish. At the same time, they must be enormous to have such high luminosities. A number of red giants can easily be seen with the naked eye, including Aldebaran in the constellation Taurus and Arcturus in Boötes.
A few rare stars are considerably bigger and brighter than typical red giants, with radii up to 1000 R⊙. Appropriately enough, these superluminous stars are called supergiants. Betelgeuse in Orion and Antares in Scorpius are two supergiants you can find in the nighttime sky. Together, giants and supergiants make up about 1% of the stars in the sky. Both giants and supergiants have thermonuclear reactions occurring in their interiors, but the character of those reactions and where in the star they occur can be quite different than for a main-sequence star like the Sun.
The remaining 9% of stars form a distinct grouping of data points toward the lower left corner of the Hertzsprung-Russell diagram. Although these stars are hot, their luminosities are quite low; hence, they must be small. They are appropriately called white dwarfs. These stars, which are so dim that they can be seen only with a telescope, are approximately the same size as Earth—more than 100 times smaller than the Sun’s diameter. No thermonuclear reactions take place within white dwarf stars. Rather, like embers left from a fire, they are the still-glowing remnants of what were once giant stars.
244
By contrast, brown dwarfs are objects that will never become stars. They are comparable in radius to the planet Jupiter. The study of brown dwarfs is still in its infancy, but it appears that there may be twice as many brown dwarfs as there are “real” stars.
ANALOGY
You can think of white dwarfs as “has-been” stars whose days of glory have passed. In this analogy, a brown dwarf is a “never-will-be.”
The existence of fundamentally different types of stars is the first important lesson to come from the H-R diagram. In Chapters 11 and 12 we will find that these different types represent various stages in the lives of stars. We will use the H-R diagram as an essential tool for understanding how stars evolve.
Question
ConceptCheck 10-17: Where on the H-R diagram are the stars with the greatest luminosity and highest temperatures?
Main-Sequence Masses and the Mass-Luminosity Relation
Years of careful, patient observations of binaries have slowly yielded the masses of many stars. As the data accumulated, an important trend began to emerge: For main-sequence stars, there is a direct correlation between mass and luminosity. The more massive a main-sequence star, the more luminous it is. Figure 10-16 depicts this mass-luminosity relation as a graph. The range of stellar masses extends from less than 0.1 of a solar mass to more than 50 solar masses. The Sun’s mass lies between these extremes.
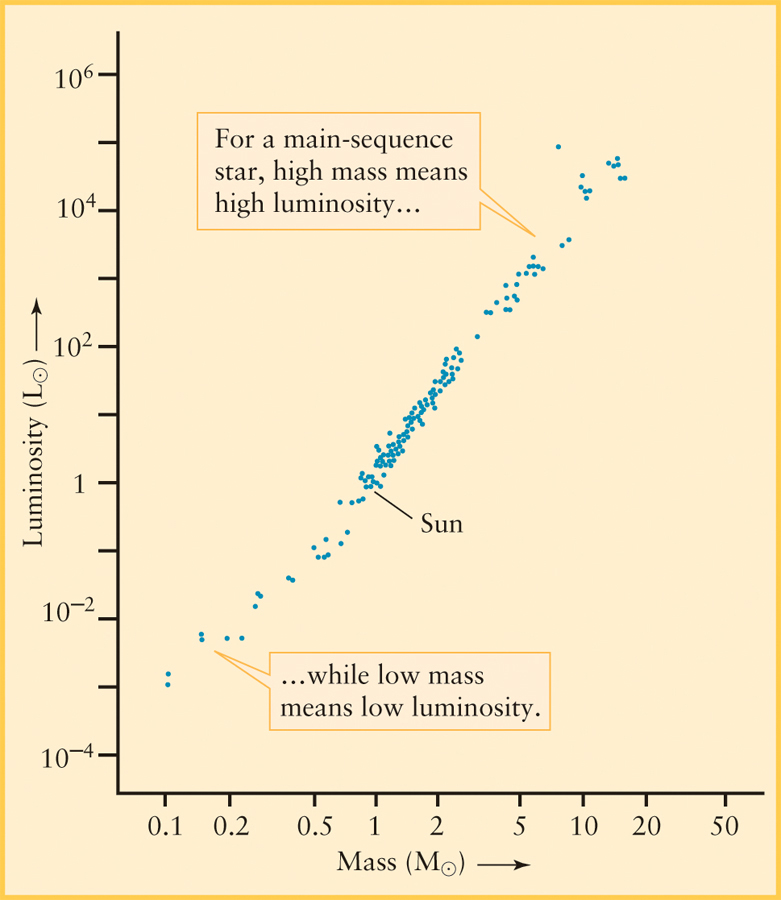
The greater the mass of a main-sequence star, the greater its luminosity, its surface temperature, and its radius.
Cosmic Connections: The Main Sequence and Masses depicts the mass-luminosity relation for main-sequence stars on an H-R diagram. This figure shows that the main sequence on an H-R diagram is a progression in mass as well as in luminosity and surface temperature. The hot, bright, bluish stars in the upper left corner of an H-R diagram are the most massive main-sequence stars. Likewise, the dim, cool, reddish stars in the lower right corner of an H-R diagram are the least massive. Main-sequence stars of intermediate temperature and luminosity also have intermediate masses.
The mass of a main-sequence star also helps determine its radius. Referring back to Figure 10-15b, we see that if we go along the main sequence from low luminosity to high luminosity, the radius of the star increases. Thus, we have the following general rule for main-sequence stars: The greater the mass of a main-sequence star, the greater its luminosity, its surface temperature, and its radius.
Why is mass the controlling factor in determining the properties of a main-sequence star? The answer is that all main-sequence stars are objects like the Sun, with essentially the same chemical composition as the Sun but with different masses. Like the Sun, all main-sequence stars shine because thermonuclear reactions at their cores convert hydrogen to helium and release energy. The greater the total mass of the star, the greater the pressure and temperature at the core, the more rapidly thermonuclear reactions take place in the core, and the greater the energy output—that is, the luminosity—of the star. In other words, the greater the mass of a main-sequence star, the greater its luminosity. This statement is just the mass-luminosity relation, which we can now recognize as a natural consequence of the nature of main-sequence stars.
Like the Sun, main-sequence stars are in a state of both hydrostatic equilibrium and thermal equilibrium. Calculations using models of a main-sequence star’s interior show that to maintain equilibrium, a more massive star must have a larger radius and a higher surface temperature. This is just what we see when we plot the curve of the main sequence on an H-R diagram (see Figure 10-15b). As you move up the main sequence from less massive stars (at the lower right in the H-R diagram) to more massive stars (at the upper left), the radius and surface temperature both increase.
CAUTION
The mass-luminosity relation we have discussed applies to main-sequence stars only. There are no simple mass-luminosity relations for giant, supergiant, or white dwarf stars. We will find that main-sequence stars evolve into giant and supergiant stars, and that some of these eventually end their lives as white dwarfs.
Question
ConceptCheck 10-18: The brightest of the main-sequence stars have what other relatively large characteristics?
245
COSMIC CONNECTIONS The Main Sequence and Masses
The main sequence is an arrangement of stars according to their mass. The most massive main-sequence stars have the greatest luminosity, largest radius, and highest surface temperature. This is a consequence of the behavior of thermonuclear reactions at the core of a main-sequence star.

246
Luminosity Classes
When carefully looking at small details of spectral lines, astronomers in the 1930s noticed subtle differences that are quite important. This caused astronomers to further classify spectra into luminosity classes. When these luminosity classes are plotted on the H-R diagram (Figure 10-17), subdivisions of the star types appear in the upper right of the diagram. Luminosity classes use arbitrary letters and Roman numbers such as I, II, and III. Luminosity classes Ia and Ib are composed of supergiants; luminosity class V includes all the main-sequence stars. The intermediate classes distinguish giant stars of various luminosities. Note that for stars of a given surface temperature (that is, a given spectral type), the higher the number of the luminosity class, the lower the star’s luminosity. These different luminosity classes represent different stages in the evolution of a star. White dwarfs are not given a luminosity class of their own, as they represent a final stage in stellar evolution in which no thermonuclear reactions take place.
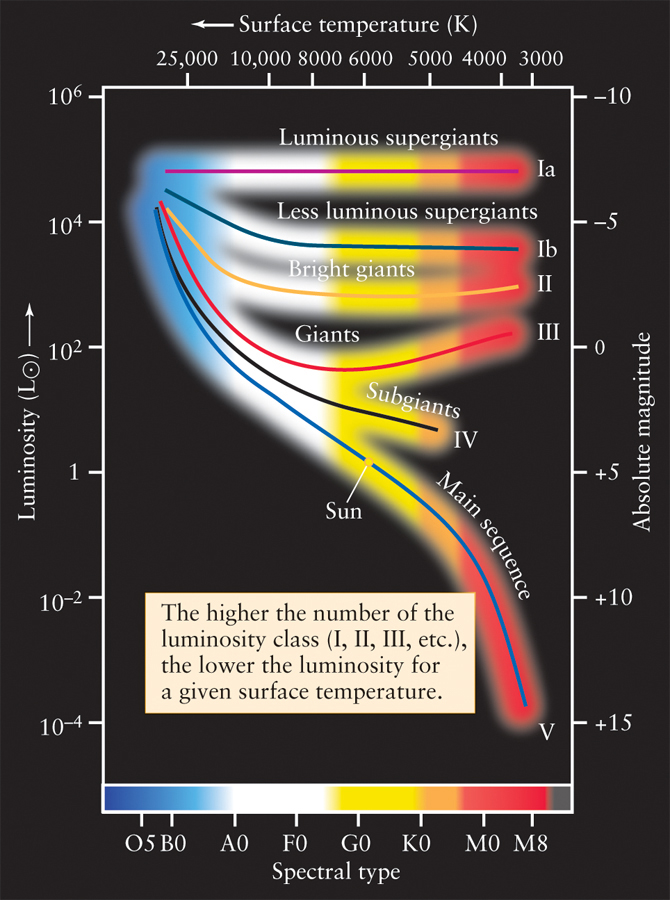
Astronomers commonly use a shorthand description that combines a star’s spectral type and its luminosity class. For example, the Sun is said to be a G2 V star. The spectral type indicates the star’s surface temperature, and the luminosity class indicates its luminosity. Thus, an astronomer knows immediately that any G2 V star is a main-sequence star with a luminosity of about 1 L⊙ and a surface temperature of about 5800 K. Similarly, a description of Aldebaran as a K5 III star tells an astronomer that it is a red giant with a luminosity of around 370 L⊙ and a surface temperature of about 4000 K.
Question
ConceptCheck 10-19: How does a K5 V star compare to a K5 II star in terms of temperature, luminosity, and radius?
Spectroscopic Parallax
Now we are in a position to put all of these ideas together to more accurately determine distances to stars. Before, the best strategy we had in determining distance was parallax, but this only works for the nearest stars. Now, using the H-R diagram, we can combine brightness, luminosity, and spectral class together to determine distance for the most distant stars. As an example, consider the star Pleione in the constellation Taurus. Its spectrum reveals Pleione to be a B8 V star (a hot, blue, main-sequence star, like the one in Figure 10-12b). An H-R diagram value for luminosity that corresponds to a B8 star would be about 190 L⊙. Given the star’s luminosity and its apparent brightness—in the case of Pleione, 3.9 × 10−13 of the apparent brightness of the Sun—we can use the inverse-square law to determine its distance from Earth.
This powerful and relatively straightforward method for determining distance, in which the luminosity of a star is found using spectral analysis, is called spectroscopic parallax. Figure 10-18 summarizes the method of spectroscopic parallax.
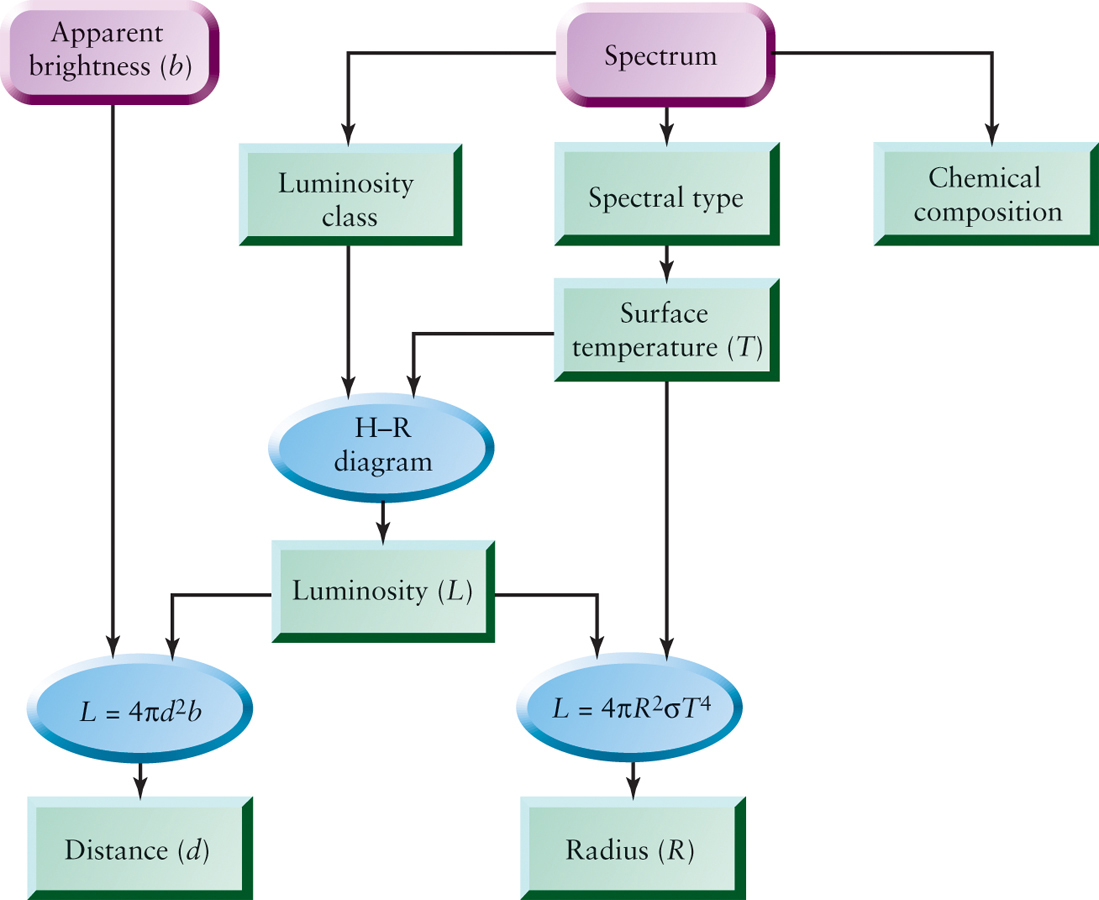
247
CAUTION
The name “spectroscopic parallax” is a bit misleading, because no parallax angle is involved! The idea is that measuring the star’s spectrum takes the place of measuring its parallax as a way to find the star’s distance. A better name for this method, although not the one used by astronomers, would be “spectroscopic distance determination.”
Spectroscopic parallax is an incredibly powerful technique. No matter how remote a star is, this technique allows astronomers to determine its distance, provided only that its spectrum and apparent brightness can be measured. Unfortunately, spectroscopic parallax has its limitations; distances to individual stars determined using this method are only accurate to at best 10%. The reason is that the luminosity classes shown in Figure 10-17 are not thin lines on the H-R diagram but are moderately broad bands. Hence, even if a star’s spectral type and luminosity class are known, there is still some uncertainty in the luminosity that we read off an H-R diagram. Nonetheless, spectroscopic parallax is often the only means that an astronomer has to estimate the distance to remote stars.
248