15-7 Observations of distant supernovae indicate that we live in an accelerating universe
At great distances, the universe’s expansion seems to be accelerating.
We have seen that the universe is expanding. But does the rate of expansion stay the same? Because there is matter in the universe, and because gravity tends to pull the bits of matter in the universe toward one another, we would expect that the expansion should slow down with time. (In the same way, a cannonball shot upward from the surface of Earth will slow down as it ascends because of Earth’s gravitational pull.) If there is a cosmological constant, however, its associated dark energy will exert an outward pressure that tends to accelerate the expansion. Which of these effects is more important?
Modeling the Expansion History of the Universe
To answer this question, astronomers study the relationship between redshift and distance for extremely remote galaxies. We see these galaxies as they were billions of years ago. If the rate of expansion was the same in the distant past as it is now, the same Hubble law should apply to distant galaxies as to nearby ones. But if the rate of expansion has either increased or decreased, we will find important deviations from the Hubble law.
To see how astronomers approach this problem, first imagine two different parallel universes. Both Universe #1 and Universe #2 are expanding at constant rates, so for both universes there is a direct proportion between recessional velocity ν and distance d as expressed by the Hubble law ν = H0d. Hence, a graph of distance versus recessional velocity for either universe is a straight line, as Figure 15-19a shows. The only difference is that Universe #1 is expanding at a slower rate than Universe #2. Hence, a galaxy at a certain distance from Earth in Universe #1 will have a slower recessional velocity than a galaxy at the same distance from Earth in Universe #2. As a result, the graph of distance versus recessional velocity for slowly expanding Universe #1 (shown in blue) has a steeper slope than the graph for rapidly expanding Universe #2 (shown in green). Keep this observation in mind: A slower expansion means a steeper slope on a graph of distance versus recessional velocity.
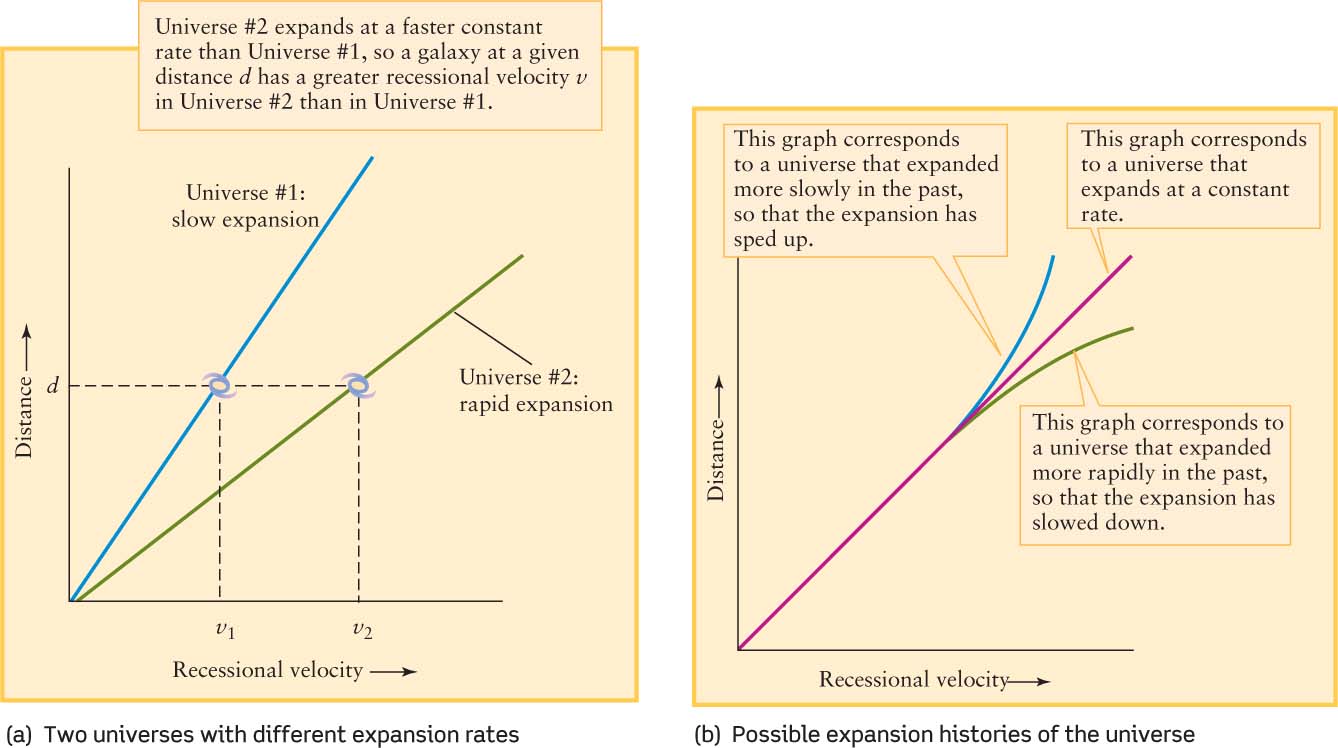
Now consider our universe and allow for the possibility that the expansion rate may change over time. If we observe very remote galaxies, we are seeing them as they were in the remote past. If the expansion of the universe in the remote past was slower or faster than it is now, the slope of the graph of distance versus recessional velocity will be different for those remote galaxies. If the expansion was slower, then the slope will be steeper for distant galaxies (shown in blue in Figure 15-19b); if the expansion was faster, the slope will be shallower for distant galaxies (shown in green in Figure 15-19b). In either case, there will be a deviation from the straight-line Hubble law (shown in purple in Figure 15-19b).
377
Question
ConceptCheck 15-14: In a universe that is expanding quickly, will the slope of a Hubble graph be steeper or shallower?
Measuring Ancient Expansion with Type Ia Supernovae
Which of the possibilities shown in Figure 15-19b represents the actual history of the expansion of our universe? In Section 15-2, we looked at the observed relationship between distance and recessional velocity for galaxies. Figure 15-4 is a plot of some representative data. The data points appear to lie along a straight line, suggesting that the rate of cosmological expansion has not changed. (Figure 15-4 is actually a graph of recessional velocity versus distance, not the other way around. But a straight line on one kind of graph will be a straight line on the other, because in either case there is a direct proportion between the two quantities being graphed.) However, the graph in Figure 15-4 was based on measurements of galaxies no farther than 400 Mpc (1.3 billion ly) from Earth, which means we are looking only 1.3 billion years into the past. The straightness of the line in Figure 15-4 means only that the expansion of the universe has been relatively constant over the past 1.3 billion years—only 10% of the age of the universe, and a relatively brief interval on the cosmic scale.
Now suppose that you were to measure the redshifts and distances of galaxies several billion light-years from Earth. The light from these galaxies has taken billions of years to arrive at your telescope, so your measurements will reveal how fast the universe was expanding billions of years ago. To do this, we need a technique that will allow us to find the distances to these very remote galaxies. One way to do this is to identify Type Ia supernovae as standard candles in such very distant galaxies. These supernovae are among the most luminous objects in the universe, and hence can be detected even at extremely large distances (see Figure 14-12). The maximum brightness of a supernova tells astronomers its distance through the inverse-square law for light, and the redshift of the supernova’s spectrum tells them its recessional velocity. Taken together, we can calculate the distance to these galaxies.
Question
ConceptCheck 15-15: What assumption must one make about Type Ia supernovae in order to use them to measure distances to galaxies?
An Accelerating Universe Filled with Dark Energy
In 1998, two prominent research groups—the Supernova Cosmology Project, led by Saul Perlmutter of Lawrence Berkeley National Laboratory, and the High-Z Supernova Search Team, led by Brian Schmidt of the Mount Stromlo and Siding Springs Observatories in Australia—reported their results from a survey of Type Ia supernovae in galaxies at redshifts of 0.2 or greater, corresponding to distances beyond 750 Mpc (2.4 billion ly). Figure 15-20 shows some of their data, along with more recent observations, on a graph of apparent magnitude versus redshift. A greater apparent magnitude corresponds to a dimmer supernova, which means that the supernova is more distant. A greater redshift implies a greater recessional velocity. Hence, this graph is basically the same as those in Figure 15-19.
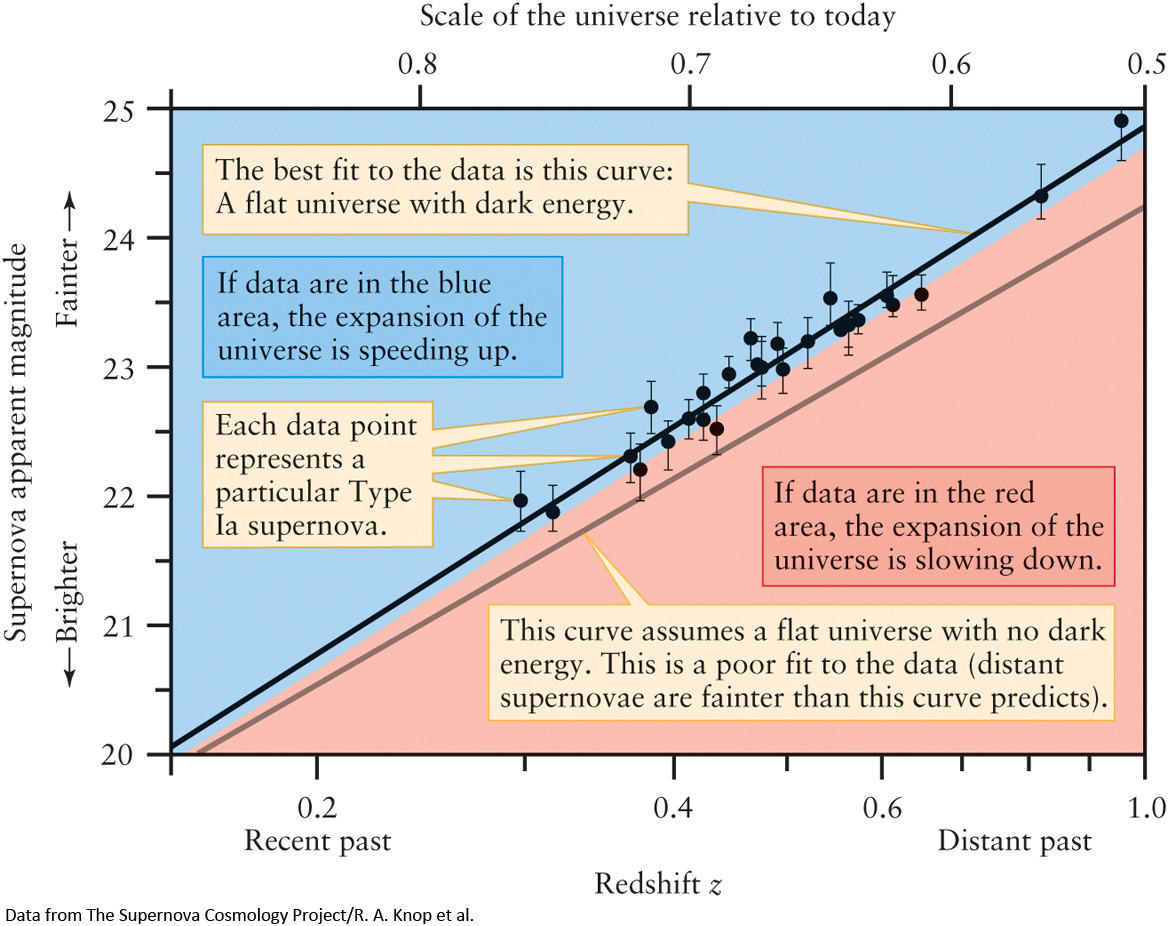
What we see here is surprising indeed: When the curve lies in the blue region of Figure 15-20, dark energy has made the expansion of the universe speed up over time. Hence, the expansion of the universe was slower in the distant past, which means that we live in an accelerating universe. Just like the blue curve in Figure 15-19b, the data in Figure 15-20 show that supernovae of a certain brightness (and hence a given distance) have smaller redshifts (and hence smaller recessional velocities) than would be the case if the expansion rate had always been the same. These data provide compelling evidence of the existence of dark energy.
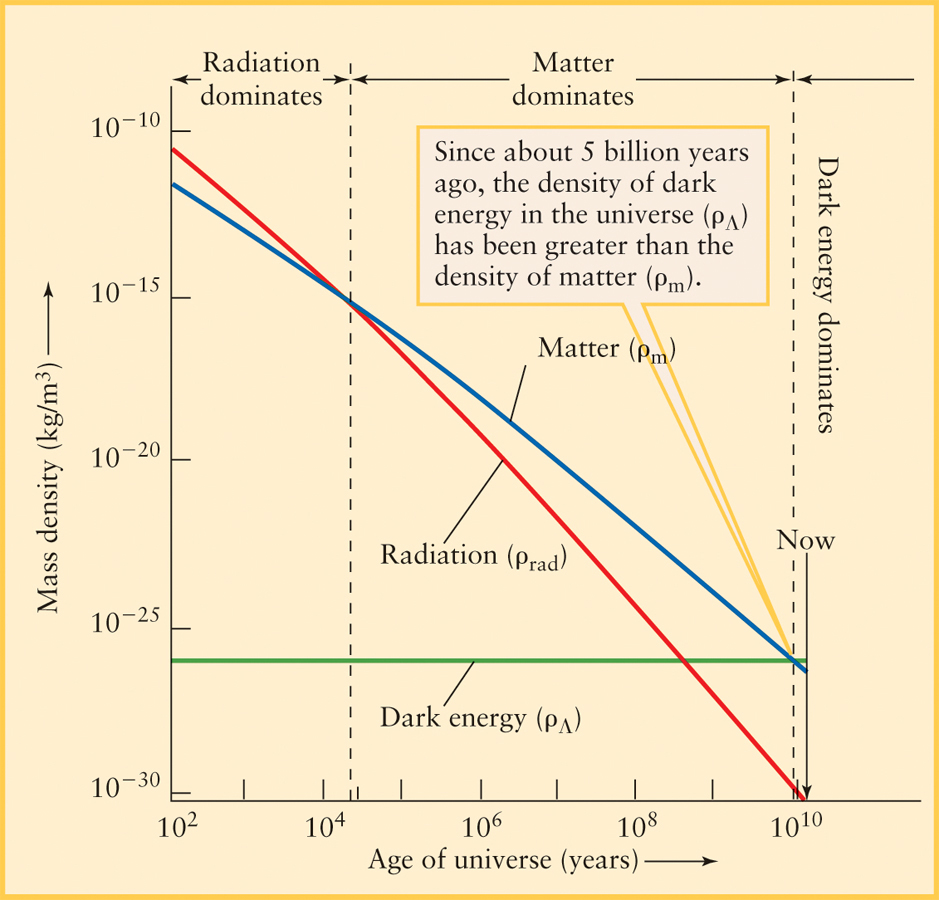
Roughly speaking, the data in Figure 15-20 indicate the relative importance of dark energy (which tends to make the expansion speed up) and gravitational attraction between galaxies (which tends to make the attraction slow down). Taken together and combined with other observations, this points to a radically different conclusion about the universe from what was suspected just a few years ago. The model we are left with is one in which the universe is suffused with a curious dark energy due to a cosmological constant. Unlike matter or radiation, whose average densities decrease as the universe expands and thins out, the average density of this dark energy remains constant throughout the history of the universe (Figure 15-21). The dark energy was relatively unimportant over most of the early history of the universe. Today, however, the density of dark energy is greater than that of matter and, in other words, we live in a dark-energy-dominated universe.
378
Yet many questions remain unanswered. What is the nature of dark matter? What actually is dark energy? Can these mysterious entities be detected and studied in the laboratory? These and other questions will probably continue to occupy cosmologists for many years to come.
We shall not cease from exploration
And the end of all our exploring
Will be to arrive where we started
And know the place for the first time.
—T. S. Eliot, Four Quartets
Question
ConceptCheck 15-16: Rank in order of greatest density for today’s universe: radiation energy, matter, and dark energy.