3-1 Astronomers of antiquity used observation and reasoning to develop astonishing advances in the study of astronomy
We sometimes perpetuate a myth that the Italian explorer Christopher Columbus proved that Earth is a sphere when he “sailed the seas of blue in the year 1492” in search of a western sailing route to the Orient for trading. Perhaps surprising, most formally educated people knew long before Columbus’s voyages that Earth is round. How did they know so long ago, before satellites could photograph Earth, that Earth is round or how large the planet is that we live on? They had come to this conclusion using a combination of observation and logical deduction, much like modern scientists.
The achievements of our ancestors still stand as impressive applications of observation and reasoning and important steps toward the development of the scientific method, particularly the calculations used to determine the size of Earth, the distances to the Sun and Moon, and the reasons for the movement of objects across the sky.
Eratosthenes Measures Earth’s Size
The earliest evidence of a round Earth is found in ancient Greek writings. No one knows specifically how Earth’s roundness was first discovered, but many travelers would have noticed that the stars, Polaris (the North Star) in particular, appeared in different positions as they traveled north and south. This observation could only occur if Earth was spherical, rather than flat.
In much the same way, it was common knowledge among the Greek philosophers that during lunar eclipses, when the Moon passes through Earth’s shadow (see Figure 1-28), the edge of the shadow is always circular. Because a sphere is the only shape that always casts a circular shadow from any angle, they correctly concluded that Earth itself is spherical.
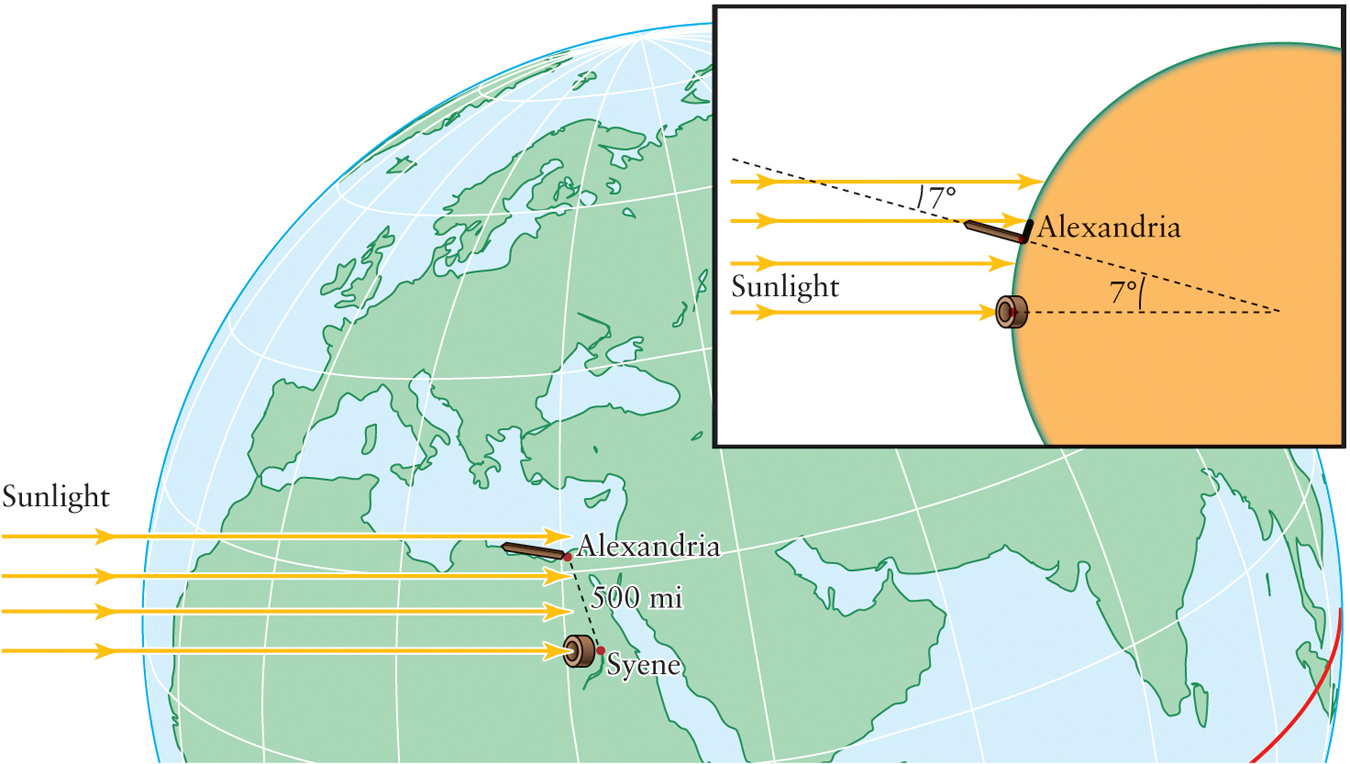
Around 240 b.c., the Greek astronomer Eratosthenes devised a way to measure Earth’s size. It was known that on the first day of summer (see Section 1.4), in the town of Syene in Egypt, near present-day Aswan, the Sun shone directly down the vertical shafts of water wells. Hence, at local noon on that day, the Sun was directly overhead as seen from Syene. Eratosthenes knew that the Sun never appeared directly overhead at his home in the Egyptian city of Alexandria, about 500 mi due north of Syene. Rather, on the summer solstice in Alexandria, the noontime Sun cast a short shadow, showing the Sun’s position was about 7° south of the zenith (Figure 3-1). If we set up a simple ratio where the 7° portion of a 360° circle is the same as a 500-mi distance, and a portion of Earth’s circumference, we get:

This calculation of 25,700 mi (41,300 km) is remarkably close to the actual value we know today of 24,901 mi (40,075 km).
Eratosthenes was only one of several brilliant astronomers to emerge from the Alexandrian school, which by his time had a distinguished tradition. Another of the Alexandrian astronomers was Aristarchus of Samos.
Aristarchus and Distances in the Solar System
Imagine how you might determine the distance to the Moon with none of our modern technologies—no satellite measurements, no laser radar ranging, not even a telescope. Aristarchus proposed a method of determining the relative distances to the Sun and Moon, perhaps as long ago as 280 b.c.
65
Aristarchus knew that the Sun, Moon, and Earth form a right triangle at the moment of first or third quarter moon, with the right angle at the location of the Moon (Figure 3-2). He estimated that, as seen from Earth, the angle between the Moon and the Sun at first and third quarters is 87°, or 3° less than a 90° right angle. Using the rules of geometry, Aristarchus concluded that the Sun is about 20 times farther from us than is the Moon. In hindsight, he was not very close, but it is impressive that Aristarchus was able to determine a reasonable method for the measurement that demonstrated that the Sun is quite a bit more distant than the Moon. Today we know that he erred in measuring angles and that the average distance to the Sun is about 390 times greater than the average distance to the Moon. Fortunately, astronomers have more precise ways to measure large distances and use various units of length, including the astronomical unit (AU) and the light-year (ly). See Box 3-1 Tools of the Astronomer’s Trade: Modern Astronomical Distances Are Often Measured in Astronomical Units or Light-Years for further explanation.
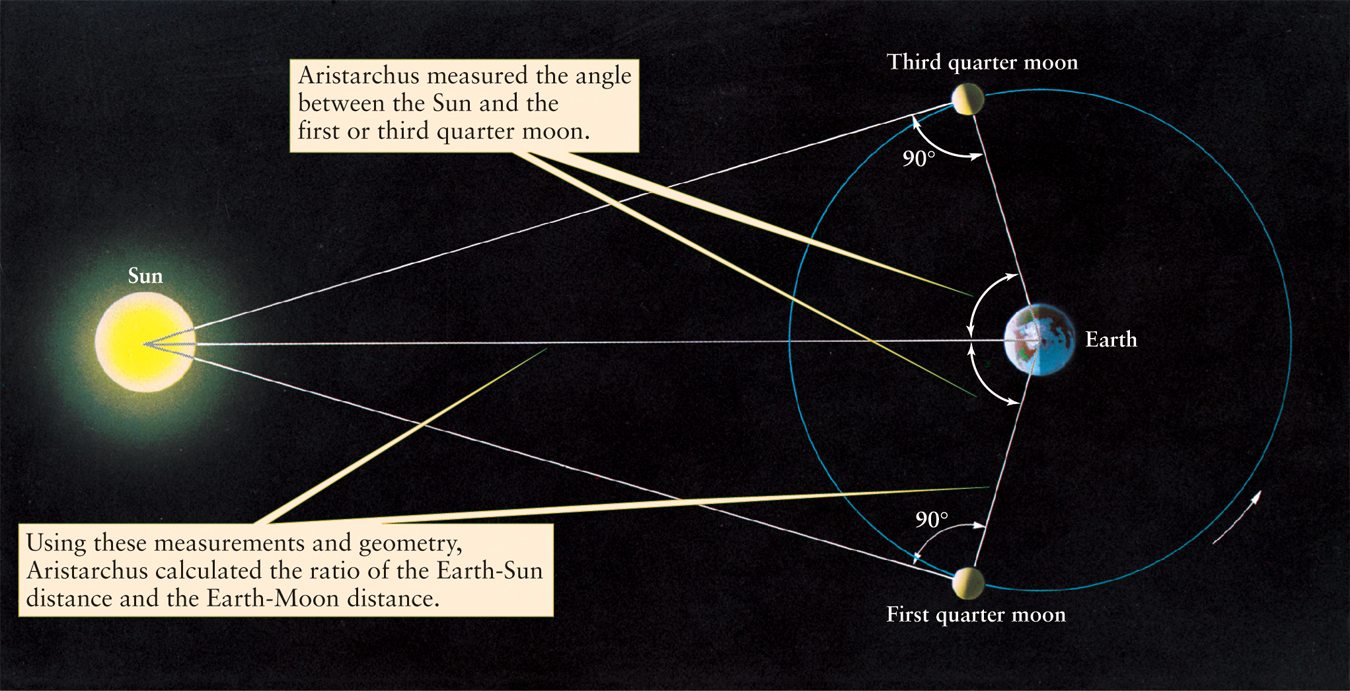
Aristarchus also made an equally bold attempt to determine the relative sizes of the Sun, Moon, and Earth. From his observations of how long the Moon takes to move through Earth’s shadow during a lunar eclipse, Aristarchus estimated the diameter of Earth to be about 3 times larger than the diameter of the Moon. To determine the diameter of the Sun, Aristarchus simply pointed out that the Sun and the Moon have the same angular size in the sky. Therefore, their diameters must be in the same proportion as their distances. In other words, because Aristarchus thought the Sun to be 20 times farther from Earth than the Moon, he concluded that the Sun must be 20 times larger than the Moon. Once Eratosthenes had measured Earth’s circumference, astronomers of the Alexandrian school could use Aristarchus’s method to estimate the diameters of the Sun and Moon as well as their distances from Earth.
66
TOOLS OF THE ASTRONOMER’S TRADE
Modern Astronomical Distances Are Often Measured in Astronomical units or Light-Years
Astronomers use many of the same units of measurement as do other scientists. They often measure lengths in meters (abbreviated m), masses in kilograms (kg), and time in seconds (s). Like other scientists, astronomers often find it useful to combine these units with powers of ten (see Appendix 9) and create new units using prefixes. As an example, the number 1000 (= 103) is represented by the prefix “kilo,” and so a distance of 1000 m is the same as 1 kilometer (1 km). Here are some of the most common prefixes, with examples of how they are used:
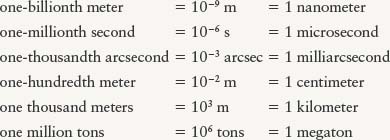
In principle, we could express all sizes and distances in astronomy using units based on the meter. Indeed, we will use kilometers to give the diameters of Earth and the Moon, as well as the Earth-Moon distance. But, while a kilometer (roughly equal to three-fifths of a mile) is an easy distance for humans to visualize, a megameter (106 m) is not. Consider this: If the length of a shoe can be measured in centimeters, does it also make sense to describe the distance between two cities in centimeters? Similarly, if we measure the distance between two cities in kilometers, does it make sense to measure the great distances between stars in kilometers? Indeed, in describing the distances between objects in the cosmos, the particular units of length used depend on just how large the distances actually are. For this reason, astronomers have devised units of measure that are more appropriate for the tremendous distances between the planets and the far greater distances between the stars.
Measuring inside our Solar System
When discussing distances across the solar system, astronomers use a unit of length called the astronomical unit (abbreviated AU). This is the average distance between Earth and the Sun:
1 AU = 1.496 × 108 km = 92.96 million mi
Thus, the average distance between the Sun and Jupiter can be conveniently stated as 5.2 AU.
Masuring Distances to the Stars
To talk about distances to the stars, astronomers use two different units of length. The light-year (abbreviated ly) is the distance that light travels in one year. This is a useful concept because the speed of light in empty space always has the same value, 3.00 × 105 km/s (kilometers per second) or 1.86 × 105 mi/s (miles per second). In terms of kilometers or astronomical units, 1 ly is given by
1 ly = 9.46 × 1012 km = 63,240 AU
This distance is roughly equal to 6 trillion mi.
CAUTION
Keep in mind that despite its name, the light-year is a unit of distance and not a unit of time. As an example, Proxima Centauri, the nearest star other than the Sun, is a distance of 4.2 ly from Earth. This means that light takes 4.2 years to travel to us from Proxima Centauri.
Physicists often measure interstellar distances in light-years because the speed of light is one of nature’s most important numbers.
Question
ConceptCheck 3-1: If Eratosthenes had found that the Sun’s noontime summer solstice altitude at Alexandria was much closer to directly overhead, would he then assume that Earth was larger, smaller, or about the same size?
Question
CalculationCheck 3-1: If Aristarchus had estimated the Sun to be 100 times farther from Earth than the Moon, how large would he have estimated the Sun to be?
The Greek Geocentric Model
 Go to Video 3-1
Go to Video 3-1
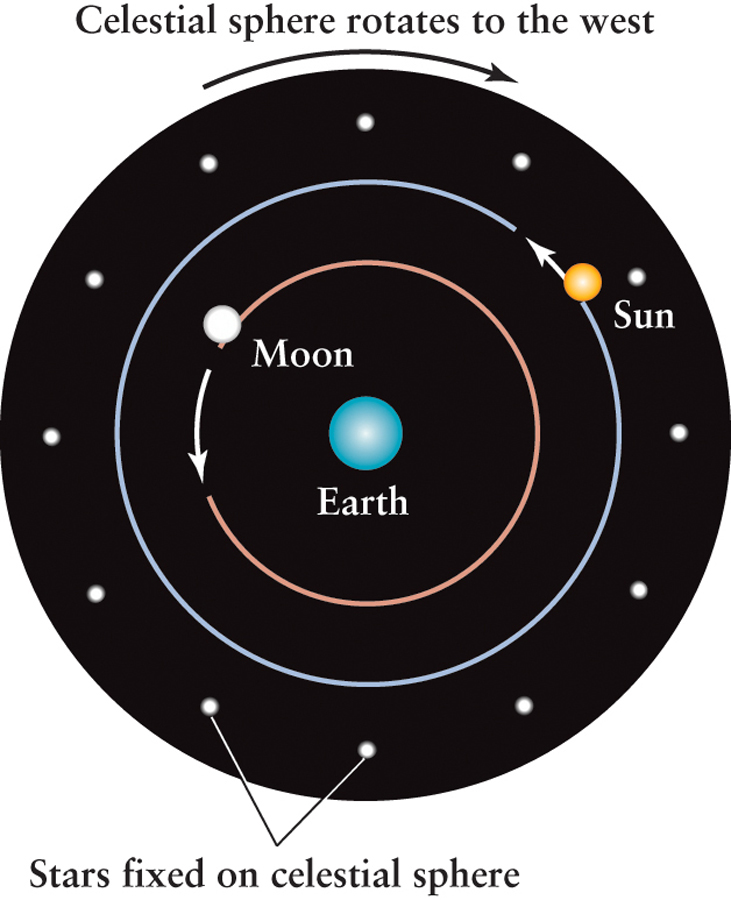
The easiest assumption to make about the cosmos is that we observers are actually stationary and everything else moves around us. This makes some sense in that you might think that if we were moving through space, we could feel it, much like we can sense the movement of a car we are riding in or a boat we are sailing in. Most Greek scholars also assumed that the Sun, the Moon, the stars, and the planets revolve about a stationary Earth, with everything rising in the east, moving across the sky, and setting in the west until it happens again tomorrow. A model of this kind, in which Earth is at the center of the universe, is called a geocentric model. Like ancient thinkers in many parts of the world, the ancient Greeks concluded that stars were brilliant points of light attached to an immense celestial sphere surrounding Earth. To explain the daily rising and setting of the stars, they assumed that the celestial sphere was real, and that it moved around the stationary Earth once a day.
67
In this Earth-centered model, the Sun and Moon both participated in this daily rotation of the sky, which explained their rising and setting motions. However, in order to be accurate, this model of how the universe works also needs to explain why the Sun and the Moon move at slightly different speeds than the stars. To explain why the Sun and Moon both slowly change their positions from night to night, compared to the fixed positions of stars, the ancient Greeks imagined that both of these objects orbit around Earth as shown in Figure 3-3.
The ancient Greeks and other cultures of that time knew of five other planets: Mercury, Venus, Mars, Jupiter, and Saturn, each of which is a bright object in the night sky. For example, when Venus is at its maximum brilliancy, it is 16 times brighter than the brightest star. (By contrast, Uranus and Neptune are quite dim and were not discovered until after the invention of the telescope.)
Like the Sun and Moon, all of the planets rise in the east and set in the west once a day. And like the Sun and Moon, from night to night the planets slowly move on the celestial sphere, that is, with respect to the background of stars. However, the character of this motion on the celestial sphere is quite different for the planets. Any model of how the universe works needs to account for all of these objects, which move at different rates.
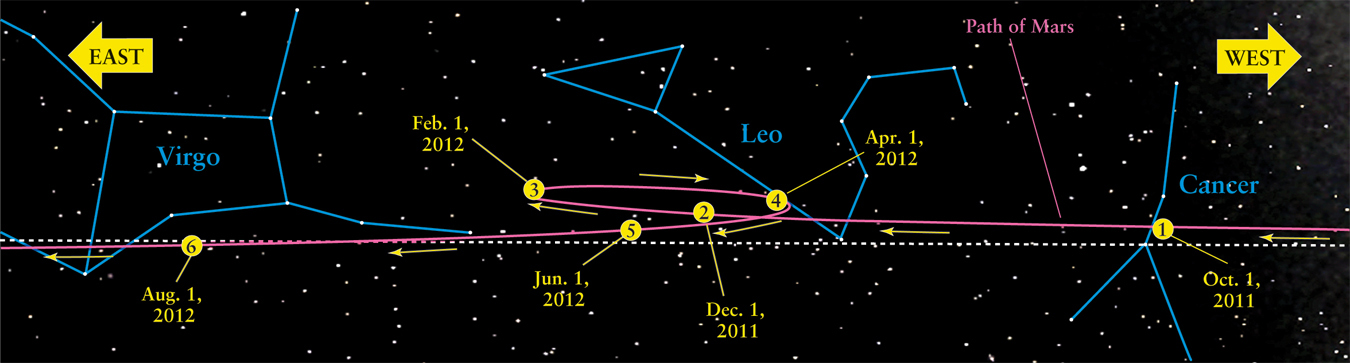
Both the Sun and the Moon always move from west to east on the celestial sphere, that is, opposite the direction in which the celestial sphere appears to rotate. The Sun follows the path called the ecliptic (see Section 1-4), while the Moon follows a path that is slightly inclined to the ecliptic (see Section 1-5). Furthermore, the Sun and the Moon each move at relatively constant speeds around the celestial sphere. (The Moon’s speed is faster than that of the Sun: It travels all the way around the celestial sphere in about a month while the Sun takes an entire year.) The planets, too, appear to move along paths that are close to the ecliptic. The difference is that each of the planets appears to wander back and forth on the celestial sphere with varying speed. As an example, Figure 3-4 shows the wandering motion of Mars with respect to the background of stars during 2011 and 2012. (This figure shows that the name planet is well deserved; it comes from a Greek word meaning “wanderer.”)
CAUTION
On a map of Earth with north at the top, west is to the left and east is to the right. Why, then, is east on the left and west on the right in Figure 3-4? The answer is that a map of Earth is a view looking downward at the ground from above, while a star map like Figure 3-4 is a view looking upward at the sky. If the constellation Leo in Figure 3-4 were directly overhead, Virgo would be toward the eastern horizon and Cancer would be toward the western horizon.
Most of the time, planets drift slowly eastward relative to the stars, just as do the Sun and Moon. For example, Figure 3-4 shows that Mars moved slowly eastward night after night from October 2011 through January 2012 and from April through August 2012. Occasionally, however, the planet will seem to stop and then back up for several weeks or months. This occasional westward movement is called retrograde motion. Mars underwent retrograde motion during February and March 2012 (see Figure 3-4), and will do so again about every 22½ months. All the planets go through retrograde motion, but at different intervals. This is quite a complication to the Earth-centered model shown in Figure 3-3, so the Greeks imagined the planets as going around, but once in a while having to stop and switch directions!
68
Whether a planet is in direct or retrograde motion, over the course of a single night you will see it rise in the east and set in the west. That is because both direct and retrograde motions are much slower than the apparent daily rotation of the sky. Hence, they are best detected by mapping the position of a planet against the background stars from night to night over a long period. Figure 3-4 is a map of just this sort.
Question
ConceptCheck 3-2: If Mars is moving retrograde, will it rise above the eastern horizon or above the western horizon?
Question
ConceptCheck 3-3: How fast is Earth spinning on its axis in the Greeks’ geocentric model?
The Ptolemaic System
Although one could imagine that the stars, planets, Moon, and Sun generally moved in a simple motion around Earth, the alternating forward and retrograde motions of the planets were not so easily explained by imagining a celestial sphere simply moving around Earth. In fact, successfully proposing a mechanism for the nonuniform motions of the five planets was one of the main challenges facing the astronomers of antiquity.
The Greeks developed many different theories to account for retrograde motion and the loops that the planets trace out against the background stars. One of the most successful and enduring explanations was advanced by Ptolemy, the last of the great Greek astronomers, during the second century a.d. (Figure 3-5a). In Ptolemy’s model, each planet is assumed to move in a small circle, whose center in turn moves in a larger circle, which is centered approximately on Earth. Both the circles rotate in the same counterclockwise sense (looking down from the north), as shown in Figure 3-5a.
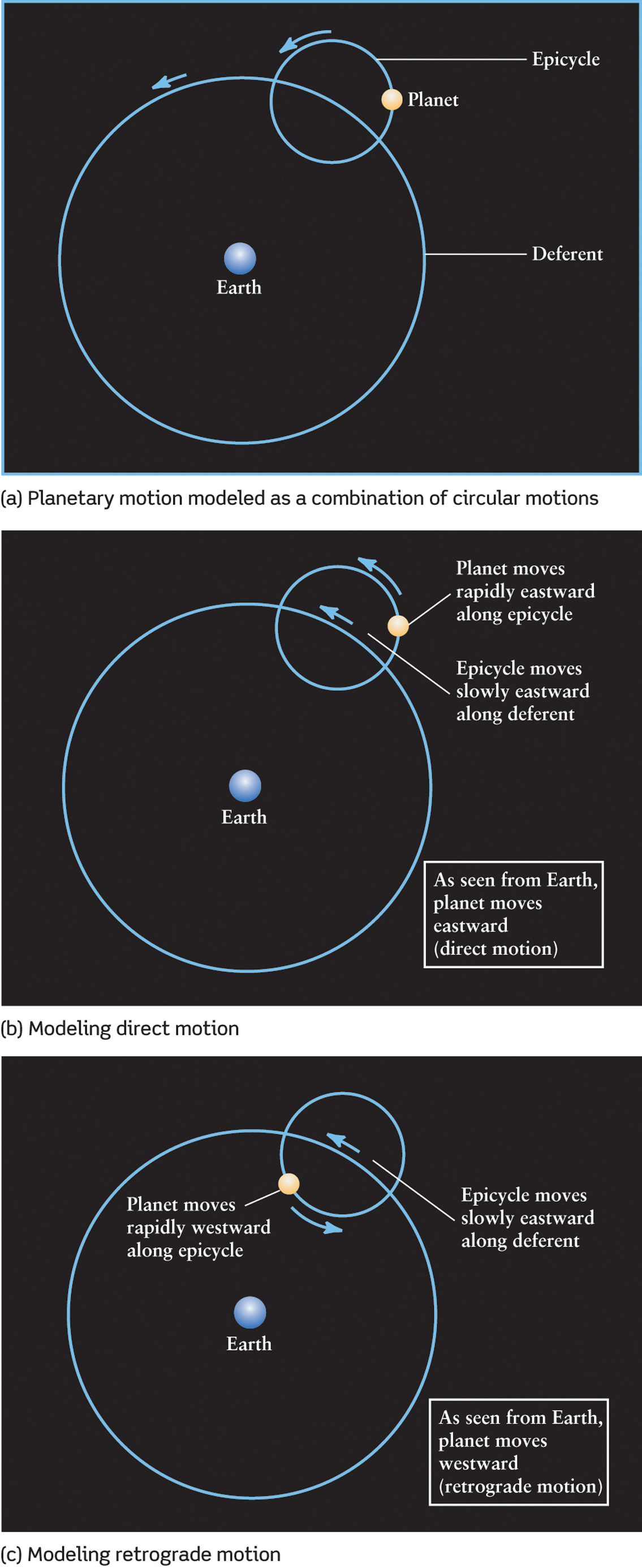
In this model, most of the time the planet will appear to drift slowly eastward as seen from Earth when compared to the background stars. However, when the planet is nearest Earth, the motion of the planet appears to slow down and halt its usual eastward movement among the constellations, and actually goes backward in retrograde (westward) motion for a few weeks or months (Figure 3-5c). Although complicated, this mechanism allowed the Greek astronomers to explain and accurately predict the retrograde loops of the planets. This incredibly complicated approach to predicting the motions of the planets was so successful that it was used for more than a thousand years as the most useful description of the workings of the heavens.
69
Question
ConceptCheck 3-4: What causes the planets to actually stop and change their direction of motion in the Ptolemaic model?