Finding the Area of a Parallelogram

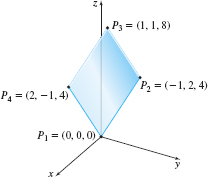
Find the area \(A\) of the parallelogram shown in Figure 49, which has vertices at the points \(P_{1}=(0, 0, 0)\), \(P_{2}=(-1, 2, 4)\), \(P_{3}=(1, 1, 8)\), and \(P_{4}=(2, -1, 4)\).

Solution The area \(A\) of a parallelogram is \(\Vert \mathbf{v} \times \mathbf{w}\Vert \), where \(\mathbf{v}\) and \(\mathbf{w}\) are two adjacent sides of the parallelogram. Be careful! Not all pairs of vertices give a side. For example, \(\overrightarrow{P_{1}~P_{3}}\) is not a side; it is a diagonal of the parallelogram. It is helpful to sketch the parallelogram before choosing \(\mathbf{v}\) and \(\mathbf{w}\). Choose \[ \begin{equation*} \mathbf{v}=\overrightarrow{P_{1}~P_{2}}= \left\langle -1,\,2,4\right\rangle =-\mathbf{i}+2\mathbf{j}+4\mathbf{k} \end{equation*} \]

729

and \[ \begin{equation*} \hbox{}\mathbf{w}=\overrightarrow{P_{1}~P_{4}} =\left\langle 2,-1,4\right\rangle =2\mathbf{i}-\mathbf{j}+4\mathbf{k} \end{equation*} \]

Then \[ \begin{equation*} \mathbf{v}\times \mathbf{w}= \left|\begin{array}{r@{\quad}r@{\quad}r} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] -1 & 2 & 4 \\[3pt] 2 & -1 & 4 \end{array}\right| =12\mathbf{i}+12\mathbf{j}-3\mathbf{k} \end{equation*} \]

The area of the parallelogram is \[ \left\Vert \mathbf{v}\times \mathbf{w}\right\Vert = \sqrt{144+144+9}= \sqrt{297} \approx 17.234~\hbox{square units} \]