Find the general equation of the plane containing the point $( 1,2,-1)$ if the vector $\mathbf{N=\,}2\mathbf{i}+3\mathbf{j}-4 \mathbf{k}$ is normal to the plane. Then use the intercepts to graph the plane.

Solution The general equation of a plane is $Ax+By+Cz=D,$ where $A,$ $B,$ and $C$ are the components of a normal vector to the plane. Since the normal is $\mathbf{N=\,}2\mathbf{i}+3\mathbf{j}-4\mathbf{k}$, we have $$2x+3y-4z=D$$

To find $D$, we use the point $(1,2,-1)$. Then $D=2(1) +3(2) -4(-1) =12.$ The general equation of the plane is $$2x+3y-4z=12$$

Figure 54 $2x+3y-4z=12$

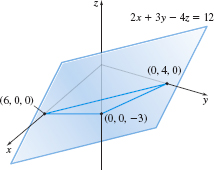
We find the intercepts by letting two variables equal zero and then solving for the third variable. For example, to find the $x$-intercept, we let $y=0$ and $z=0.$ Then $2x=12$ or $x=6.$ Similarly, the $y$-intercept is $4$ and the $z$-intercept is $-3.$ Figure 54 illustrates how the intercepts are used to graph the plane.