Identify the cylinder defined by the equation $y^{2}=8z$. Describe how it can be generated.

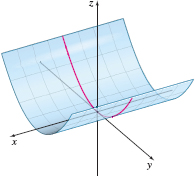
Figure 72 $y^{2}=8z$

Solution $y^{2}=8z$ is an equation of a parabolic cylinder. Since $x$ is the missing variable, the cylinder is generated by moving a line that is perpendicular to the $yz$-plane along the parabola $y^{2}=8z.$ See Figure 72