Divide both sides of the equation by $36,$ obtaining $$\frac{x^{2}}{9}-\frac{y^{2}}{2}+\frac{z^{2}}{4}=1$$

Figure 73 $\dfrac{x^2}{9} - \dfrac{y^2}{2} + \dfrac{z^2}{4} =1$

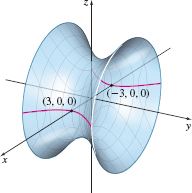
This equation has three squared variables, one term negative, with $1$ on the right, so it represents a hyperboloid of one sheet. Since the $y$ term is negative, the $y$-axis is the axis of the hyperboloid of one sheet. See Figure 73.

The intercepts are $(3,0,0)$, $(-3,0,0)$, $(0,0,2)$, and $(0,0,-2)$. There are no $y$-intercepts.

The trace in the $xz$-plane is the ellipse $\dfrac{x^{2}}{9}+\dfrac{z^{2}}{4} =1$, and all traces parallel to the $xz$-plane are also ellipses. The trace in the $xy$-plane is the hyperbola $\dfrac{x^{2}}{9}-\dfrac{y^{2}}{2}=1$. The trace in the $yz$-plane is the hyperbola $-\dfrac{y^{2}}{2}+\dfrac{z^{2} }{4}=1$. Traces parallel to the $xy$- and $yz$-planes are also hyperbolas. The $y$-axis is the axis of the hyperboloid of one sheet.

We begin by writing the equation as \[ \begin{equation*} x^{2}=\frac{y^{2}}{9}+\frac{z^{2}}{4} \end{equation*}

Figure 74 $x^{2}=\dfrac{y^2}{9}+\dfrac{z^2}{4}$

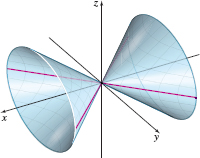
Observe that the equation has three variables, all of which are squared, and no constant. This is the equation of an elliptic cone. See Figure 74.

751

The vertex of the cone is at the origin $( 0,0,0) .$

The trace of the elliptic cone in the $yz$-plane is the origin. Traces parallel to the $yz$-plane are ellipses centered on the $x$-axis. The trace in the $xy$-plane consists of the pair of intersecting lines $x=\pm \dfrac{y }{3}$, and the trace in the $xz$-plane consists of the pair of intersecting lines $x=\pm \dfrac{z}{2}$.

Figure 75 $( x-2) ^{2}+z^{2}=4$

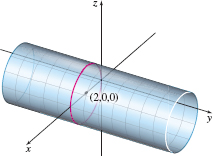
Since the $y$ variable is missing, the surface is a cylinder. To identify it, we complete the square in $x$: \[ \begin{eqnarray*} x^{2}+z^{2}-4x &=&0 \\ ( x-2) ^{2}+z^{2} &=&4 \end{eqnarray*}

This is the equation of a right circular cylinder with a radius $2$. The trace in the $xz$-plane is a circle of radius $2$ and with its center at the point $( 2,0,0)$. See Figure 75.