Figure

EXAMPLE 8Using Standard Basis Vectors to Model a Problem

An airplane has an air speed of $400$ km $/$ h and is headed east. There is a northwesterly wind of $80$ km $/$ h. (Northwesterly winds blow toward the southeast.)

(a) Find a vector representing the velocity of the airplane in the air.
(b) Find a vector representing the wind velocity.
(c) Find a vector representing the velocity of the airplane relative to the ground.
(d) Find the true speed of the airplane.

Figure 31

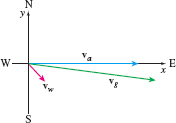
We use a two-dimensional coordinate system with the direction north along the positive $y$ -axis. Then the direction east is along the positive $x$ -axis.

Using a scale of $1~\hbox{unit} = 1$ km $/$ h, define $\begin{eqnarray*} \mathbf{v}_{\mathrm{a}} &=& \hbox{Velocity of the airplane in the air}\\[2pt] \mathbf{v}_{\mathrm{w}} &=& \hbox{Velocity of the wind}\\[2pt] \mathbf{v}_{\mathrm{g}} &=& \hbox{Velocity of the airplane relative to the ground} \end{eqnarray*}$

Figure 32

Figure 31 shows the vectors $\mathbf{v}_{a},$ $\mathbf{v}_{w},$ $\mathbf{v}_{g}.$

The vector $\mathbf{v}_{\rm{a}}$ has magnitude $400$ and direction $\mathbf{i}$ , so $\mathbf{v}_{\mathrm{a}}$ = 400i.
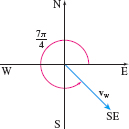
The vector $\mathbf{v}_{\mathrm{w}}$ has magnitude $80$ and makes an angle of $\dfrac{7\pi}{4}$ with the positive $x$ -axis, as shown in Figure 32. Since the magnitude of $\mathbf{v}_{\rm{w}}$ is 80, $\mathbf{v}_{\rm{w}} = 80\left(\cos \dfrac{7\pi}{4}\mathbf{i} + \sin \dfrac{7\pi}{4}\mathbf{j}\right) = 80 \left(\dfrac{\sqrt{2}}{2}\mathbf{i} - \dfrac{\sqrt{2}}{2}\mathbf{j}\right) = 40\sqrt{2}\mathbf{i} - 40\sqrt{2}\mathbf{j}$
The velocity $\mathbf{v}_{\mathrm{g}}$ of the airplane relative to the ground is the resultant of $\mathbf{v}_{\rm{a }}$ and $\mathbf{v}_{\rm{w}}.$ $\mathbf{v}_{\mathrm{g}} = \mathbf{v}_{\mathrm{a}} + \mathbf{v}_{\mathrm{w}} = 400\ \mathbf{i} + \left[ 40\sqrt{2} \mathbf{i} - 40\sqrt{2} \mathbf{j}\right] = (400 + 40\sqrt{2}) \mathbf{i} - 40\sqrt{2} \mathbf{j}$
The true speed of the airplane is the magnitude of the vector $\mathbf{v}_{\mathrm{g}}.$ $\left\Vert \mathbf{v}_{\mathrm{g}}\right\Vert =\sqrt{(400 + 40\sqrt{2})^{2} + (40\sqrt{2})^{2}}\approx 460.060$

The true speed of the airplane is approximately $460.060 \,\rm{km/h}$ .