Finding the Tension in Cable

A commercial air conditioner weighing 8600 lb is suspended from two cables, as shown in Figure 33. What is the tension in each cable?

711

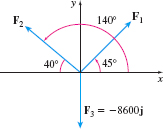
Solution We represent the cables and the air conditioner with a force diagram, as shown in Figure 34.

The tension in each cable is the magnitude of \(\Vert\mathbf{F}_{1}\Vert \) and \(\Vert\mathbf{F}_{2}\Vert,\) respectively. The weight of the air conditioner is \(\Vert\mathbf{F}_{3}\Vert = 8600~\text{lb}\). \[ \begin{eqnarray*} \mathbf{F}_{1} &=& \Vert\mathbf{F}_{1}\Vert \left( \cos 45^{\circ}\mathbf{i} + \sin 45^{\circ}\mathbf{j}\right) = \Vert\mathbf{F}_{1}\Vert \left(\dfrac{\sqrt{2}}{2} \mathbf{i} + \dfrac{\sqrt{2}}{2} \mathbf{j}\right) \\[4pt] \mathbf{F}_{2} &=& \Vert \mathbf{F}_{2}\Vert \left(\cos 140^{\circ} \mathbf{i} + \sin 140^{\circ} \mathbf{j}\right) \\[4pt] \mathbf{F}_{3} &=& -8600 \mathbf{j} \end{eqnarray*} \]

For the air conditioner to be in static equilibrium, the sum of the forces acting on it must equal \(\mathbf{0}\). That is, \[ \begin{eqnarray*} \mathbf{F}_{1} + \mathbf{F}_{2} + \mathbf{F}_{3} &=& \left(\dfrac{\sqrt{2}}{2} \Vert\mathbf{F}_{1}\Vert \mathbf{i} + \dfrac{\sqrt{2}}{2} \Vert\mathbf{F}_{1}\Vert \mathbf{j}\right)\\[6pt] &&+ \left(\cos 140^{\circ} \Vert\mathbf{F}_{2}\Vert \mathbf{i} + \sin 140^{\circ} \Vert\mathbf{F}_{2}\Vert \mathbf{j}\right) -8600\mathbf{j} = \mathbf{0} \end{eqnarray*} \]

Since both the \(\mathbf{i}\) and \(\mathbf{j}\) components equal \(0,\) we have a system of two equations: \[ \begin{equation*} \left\{ \begin{array}{rcl@{\hspace*{5pc}}r@{}} \dfrac{\sqrt{2}}{2}\Vert\mathbf{F}_{1}\Vert + \cos 140^{\circ} \Vert\mathbf{F}_{2}\Vert &=& 0 & \hbox{(1)} \\ \dfrac{\sqrt{2}}{2}\Vert \mathbf{F}_{1}\Vert + \sin 140^{\circ} \Vert\mathbf{F}_{2}\Vert -8600 &=& 0 & \hbox{(2)} \end{array} \right. \end{equation*} \]

We solve equation (1) for \(\left\Vert \mathbf{F}_{1}\right\Vert\): \[ \begin{equation*} \Vert\mathbf{F}_{1}\Vert = -\dfrac{2\cos 140^{\circ} \Vert\mathbf{F}_{2}\Vert}{\sqrt{2}} \tag{3} \end{equation*} \]

and substitute the result into equation (2). \[ \begin{eqnarray*} \dfrac{\sqrt{2}}{2}\left(-\dfrac{2\cos 140^{\circ} \Vert\mathbf{F}_{2}\Vert}{\sqrt{2}}\right) + \sin 140^{\circ} \Vert\mathbf{F}_{2}\Vert -8600 &=& 0 \\[4pt] \left[-\cos 140^{\circ} + \sin 140^{\circ} \right] \Vert\mathbf{F}_{2}\Vert &=& 8600 \\[4pt] \Vert \mathbf{F}_{2}\Vert &=& \dfrac{8600}{\sin 140^{\circ} - \cos 140^{\circ}}\approx 6104 \end{eqnarray*} \]

Then from (3) \[ \begin{equation*} \Vert\mathbf{F}_{1}\Vert = -\dfrac{2\cos 140^{\circ} \Vt\mathbf{F}_{2}\Vert}{\sqrt{2}}\approx -\dfrac{2\cos 140^{\circ}}{\sqrt{2}}(6104) \approx 6613 \end{equation*} \]