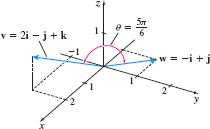
Finding the Dot Product of Two Vectors

Find the angle between the vectors \(\mathbf{v}=2\mathbf{i}-\mathbf{j}+ \mathbf{k}\) and \(\mathbf{w}=- \mathbf{i}+\mathbf{j}\).

Solution We find \(\mathbf{v}\,{\cdot}\, \mathbf{w}\), \(\Vert \mathbf{v} \Vert ,\) and \(\Vert \mathbf{w}\Vert.\) \[ \begin{eqnarray*} \mathbf{v}\,{\cdot}\, \mathbf{w} &=&(2) (-1) +(-1) (1) +(1) (0) =-2-1+0=-3 \\[4pt] \Vert \mathbf{v}\Vert &=&\sqrt{2^{2}+(-1) ^{2}+1^{2}}=\sqrt{6} \\[4pt] \Vert \mathbf{w}\Vert &=&\sqrt{(-1) ^{2}+1^{2}}=\sqrt{2} \end{eqnarray*} \]

Then if \(\theta\) is the angle between \(\mathbf{v}\) and \(\mathbf{w}\), \[ \begin{equation*} \cos \theta =\dfrac{\mathbf{v}\,{\cdot}\, \mathbf{w}}{\Vert \mathbf{v}\Vert \Vert \mathbf{w}\Vert }=\dfrac{-3}{( \sqrt{6}) (\sqrt{2}) }= \dfrac{-3}{\sqrt{12}}=-\dfrac{\sqrt{3}}{2} \end{equation*} \]

Since \(0\leq \theta \leq \pi\), the angle \(\theta\) between \(\mathbf{v}\) and \(\mathbf{w}\) is \(\dfrac{5\pi}{6}\) radians. See Figure 36.