Computing Work

Figure 43 shows a man pushing on a lawn mower handle with a force of 30 lb. How much work is done in moving the lawn mower a distance of 75 ft if the handle makes an angle of \(60^{\circ }\) with the ground?

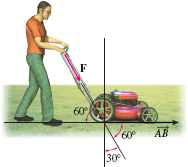
Solution We set up the coordinate system so that the lawn mower is moved from \((0,0)\) to \((75,0)\). Then the motion occurs along \( \skew5\overrightarrow{\it AB}=75\,\mathbf{i}\). The force vector \(\mathbf{F}\), as shown in Figure 44, makes an angle of \(300^\circ\) to the positive \(x\)-axis. Since \(\Vert \mathbf{F} \Vert = 30\), \(\mathbf{F}\) is given by \[ \begin{equation*} \mathbf{F}=30[ (\cos 300^{\circ })\mathbf{i}+(\sin 300^{\circ })\mathbf{ j}] =30\left[ \dfrac{1}{2}\mathbf{i}-\dfrac{\sqrt{3}}{2}\mathbf{j} \right] =15\mathbf{i}-15\sqrt{3}\mathbf{j} \end{equation*} \]

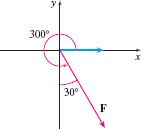
Then the work \(W\) done is \[ W=\mathbf{F}\,{\cdot}\, \skew5\overrightarrow{\it AB}=(15\mathbf{i}-15\sqrt{3}\mathbf{j} )\,{\cdot}\, 75\mathbf{i}=1125 \hbox{ft-lb} \]