EXAMPLE 3Graphing a Vector Function
Graph the curve C traced out by the vector function r(t)=(2+3t)i+(3−t)j+2tk
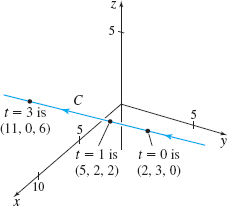
Figure 5 r(t)=(2+3t)i+(3−t)j+2tk
Solution The components of r=r(t) are the parametric equations x(t)=2+3ty(t)=3−tz(t)=2t
These are the parametric equations of a line in space containing the point (2,3,0) (corresponding to t=0) and in the direction of the vector 3i−j+2k. Solving for t, we obtain the symmetric equations of this line x−23=y−3−1=z2
Since r(0)=2i+3j and r(1)=5i+2j+2k, the positive direction of C is given by r(1)−r(0)=3i−j+2k. See Figure 5.