EXAMPLE 1Finding the Angle Between a Tangent Vector to a Helix and the Direction k
Show that the acute angle between the tangent vector to the helix r(t)=costi+sintj+tk0≤t≤2π
and the direction k is π4 radian.
Solution A tangent vector at any point on the helix is given by r′(t)=−sinti+costj+k
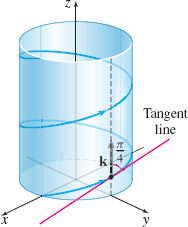
Figure 10 r(t)=costi+sintj+tk,0≤t≤2π
Then ‖
The cosine of the acute angle \theta between \mathbf{r}^{\prime} (t) and \mathbf{k} is \begin{eqnarray*} &&\cos \theta =\frac{\mathbf{r}^{\prime} (t)\,{\cdot}\, \mathbf{k}}{\left\Vert \mathbf{r} ^{\prime} (t)\right\Vert \left\Vert \mathbf{k}\right\Vert }=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\qquad \color{#0066A7}{\hbox{$\mathbf{r}^{\prime} (t)\,{\cdot}\, \mathbf{k} = 1$}}\\ \end{eqnarray*}
So, \theta =\dfrac{\pi }{4} radian. See Figure 10.