Finding a Unit Tangent Vector to a Curve

Show that the unit tangent vector \(\mathbf{T}(t)\) to the circle of radius \(R\) \begin{equation*} \mathbf{r}(t)=R\cos t\mathbf{i}+R\;\sin t\mathbf{j}\quad 0\leq t\leq 2\pi \end{equation*}

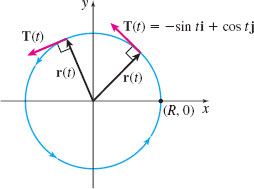
is everywhere orthogonal to \(\mathbf{r}(t).\) Graph \(\mathbf{r}=\mathbf{r}( t)\) and \(\mathbf{T}=\mathbf{T}( t).\)

Solution We begin by finding \(\mathbf{r}^{\prime} (t)\) and \(\left\Vert \mathbf{r}^{\prime} (t)\right\Vert\): \begin{eqnarray*} \mathbf{r}^{\prime} (t)& =&\dfrac{d}{dt}( R\cos t) \mathbf{i}+ \dfrac{d}{dt}( R\;\sin t) \mathbf{j}=-R\;\sin t\mathbf{i}+R\cos t\mathbf{j} \\[6pt] \left\Vert \mathbf{r}^{\prime} (t)\right\Vert & =&\sqrt{(-R\;\sin t)^{2}+(R\cos t)^{2}}=R \end{eqnarray*}

Then the unit tangent vector is \begin{equation*} \mathbf{T}(t)=\frac{\mathbf{r}^{\prime} (t)}{\left\Vert \mathbf{r}^{\prime} (t)\right\Vert }=\dfrac{-R\;\sin t\mathbf{i}+R\;\cos t\mathbf{j}}{R}=-\!\sin t\mathbf{i}+\cos t\mathbf{j} \end{equation*}

To determine whether \(\mathbf{r}( t)\) is orthogonal to \(\mathbf{T}( t), \) we find their dot product. \begin{equation*} \mathbf{T}(t)\,{\cdot}\, \mathbf{r}(t)=( -\!\sin t\mathbf{i}+\cos t\mathbf{j}) \,{\cdot}\, ( R\;\cos t\mathbf{i}+R\;\sin t\mathbf{j}) =-R\;\sin t\cos t+R\;\sin t\cos t=0 \end{equation*}

for all \(t.\) That is, \(\mathbf{T}(t)\) is everywhere orthogonal to \(\mathbf{r}(t)\), as shown in Figure 11.