Finding the Arc Length of a Circle and a Helix

Find the arc length of:

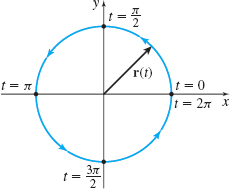
(a) The circle \(\mathbf{r}(t)=R\;\cos t\mathbf{i}+R\;\sin t\mathbf{j}\) from \(t=0\) to \(t=2\pi \)

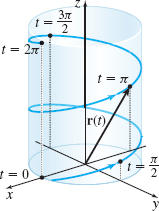
(b) The circular helix \(\mathbf{r}(t)=R\;\cos t\mathbf{i}+R\;\sin t\mathbf{j}+t\mathbf{k}\) from \(t=0\) to \(t=2\pi \)

Solution (a) We begin by finding \(\mathbf{r^{\prime} }( t)\) and \(\left\Vert \mathbf{r^{\prime} }( t) \right\Vert \): \[ \mathbf{r}^{\prime} (t)=-R\;\sin t\mathbf{i}+R\;\cos t\mathbf{j}\qquad \left\Vert \mathbf{r}^{\prime} (t)\right\Vert =\sqrt{(-R\;\sin t)^{2}+(R\;\cos t)^{2}}=R \]

Now we use the formula for arc length. \begin{equation*} s=\int_{a}^{b}\left\Vert \mathbf{r}^{\prime} (t)\right\Vert dt=\int_{0}^{2\pi }Rdt=\big[ R\hbox{ }t\big] _{0}^{2\pi }=2\pi R \end{equation*}

which is the familiar formula for the circumference of a circle. See Figure 15.

(b) We begin by finding \(\mathbf{r^{\prime} }( t)\) and \(\left\Vert \mathbf{r^{\prime} }( t) \right\Vert.\) \begin{eqnarray*} \mathbf{r}^{\prime} (t) &=&-R\;\sin t\mathbf{i}\,{+}\,R\;\cos t\mathbf{j}+\mathbf{k},\\[6pt] \left\Vert \mathbf{r}^{\prime} (t)\right\Vert &=& \sqrt{\!(-R\;\sin t)^{2}\,{+}\,(R\;\cos t)^{2}\,{+}\,1^{2}}\,{=}\,\sqrt{R^{2}\,{+}\,1} \end{eqnarray*}

Then \begin{equation*} ~s=\int_{a}^{b}\left\Vert \mathbf{r}^{\prime} ( t) \right\Vert dt=\int_{0}^{2\pi }\sqrt{R^{2}+1}~dt=\left[ \sqrt{R^{2}+1}\,t\right] _{0}^{2\pi }=2\pi \sqrt{R^{2}+1} \end{equation*}

See Figure 16.