Figure 17 $\mathbf{r}( t) =2\cos t\mathbf{i}+3\sin t\mathbf{j,} \\ 0\leq t\leq \dfrac{\pi }{2}$

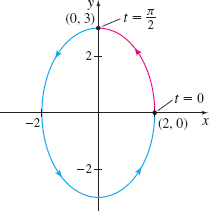
Use technology to find the arc length $s$ of the ellipse shown in Figure 17 traced out by the vector function $\mathbf{r}( t) =2\cos t\mathbf{i}+3\sin t\mathbf{j}$ from $t=0$ to $t=\dfrac{\pi }{2}.$

Solution We begin by finding $\mathbf{r^{\prime} }( t)$ and $\left\Vert \mathbf{r^{\prime} }( t) \right\Vert .$ $$\mathbf{r}^{\prime} (t)=-2\sin t\mathbf{i}+3\cos t\mathbf{j}\qquad \left\Vert \mathbf{r}^{\prime} (t)\right\Vert =\sqrt{4\sin ^{2}t+9\cos ^{2}t}$$

Now we use the formula for arc length. $$\begin{equation*} s=\int_{a}^{b}\left\Vert \mathbf{r}^{\prime} (t)\right\Vert dt=\int_{0}^{\pi /2}\sqrt{4\sin ^{2}t+9\cos ^{2}t}\,dt \end{equation*}$$

This is an integral that has no antiderivative in terms of elementary functions. To obtain a numerical approximation to the arc length, we use a CAS or a graphing utility.

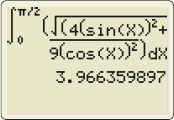
When entering the integral in WolframAlpha, we find $$\begin{equation*} \int_{0}^{\pi /2}\sqrt{4\sin ^{2}t+9\cos ^{2}t}\,dt\approx 3.96636 \end{equation*}$$

Figure 18

If we use a TI-84 to find the value of this integral, we obtain the same result. The screen shot is given in Figure 18.