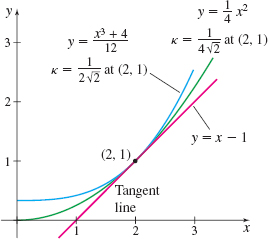
Finding the Curvature of Plane Curves

(a) Find an equation of the tangent line to the graph of the parabola \(f(x)\;=\;\dfrac{1}{4}x^{2}\) at the point \((2,1).\)

(b) What is the curvature of the graph of \(f\) at the point \((2,1)?\)

(c) Find an equation of the tangent line to the graph of \(g(x)\;=\;\dfrac{x^{3}+4}{12}\) at the point \((2,1).\)

(d) What is the curvature of the graph of \(g\) at the point \(( 2,1)?\)

(e) Graph both curves and their tangent lines.

780

Solution (a) \(f(x)\;=\;\dfrac{1}{4}x^{2};\) \(f^{\prime} (x)\;=\;\dfrac{1}{2}x\). An equation of the tangent line to the graph of \(f\) at the point \(( 2,1)\) is \begin{eqnarray*} y-1 &=&1\,{\cdot}\, (x-2)\qquad \color{#0066A7}{f^{\prime} (2)\;=\;{1}} \\[4pt] y &=&x-1 \end{eqnarray*}

(b) \(f^{\prime \prime} (x)\;=\;\dfrac{1}{2};\quad f^{\prime} (2)\;=\;1;\quad f^{\prime \prime} (2)\;=\;\dfrac{1}{2}\). We use formula (9) and evaluate \(\kappa\) at \(x=2\). \begin{equation*} \kappa\;=\;\dfrac{\left\vert f^{\prime \prime} ( 2) \right\vert }{ \left( 1+\left[ f^{\prime} ( 2) \right] ^{2}\right) ^{3/2}}=\dfrac{ \dfrac{1}{2}}{( 1+1) ^{3/2}}=\dfrac{1}{2\,{\cdot}\, 2\sqrt{2}}=\dfrac{1 }{4\sqrt{2}}\approx 0.177 \end{equation*}

(c) \(g(x)\;=\;\dfrac{x^{3}+4}{12};\quad g^{\prime} (x)\;=\;\dfrac{3x^{2}}{12}=\dfrac{x^{2}}{4}\). An equation of the tangent line to the graph of \(g\) at the point \((2,1)\) is \begin{eqnarray*} y-1 &=&1\,{\cdot}\, ( x-2)\qquad \color{#0066A7}{g^{\prime} (2)\;=\;{1}} \\[4pt] y &=&x-1 \end{eqnarray*}

(d) \(g^{\prime \prime} (x)\;=\;\dfrac{x}{2};\quad g^{\prime} (2)\;=\;1;\quad g^{\prime \prime} (2)\;=\;1\). The curvature \(\kappa\) at the point \((2,1)\) is \begin{equation*} \kappa\;=\;\dfrac{\vert g^{\prime \prime} ( 2) \vert }{ ( 1+[ g^{\prime} ( 2) ] ^{2}) ^{3/2}}=\dfrac{1 }{( 1+1) ^{3/2}}=\dfrac{1}{2\sqrt{2}}\approx 0.354 \end{equation*}

(e) The functions \(f\) and \(g\) are graphed in Figure 20. Both graphs have the same tangent line at \((2,1),\) but the tangent line to the graph of \(y=\dfrac{1}{4}x^{2}\) at \((2,1)\) turns more slowly \((\kappa \approx 0.177)\) than the tangent line to the graph of \(y=\dfrac{x^{3}+4}{12}\) at \((2,1)\) \((\kappa \approx 0.354)\).