Finding Velocity, Acceleration, and Speed

Find the velocity \(\mathbf{v}\), acceleration \(\mathbf{a}\), and speed \(v\) of a particle that is moving along:

(a) the plane curve \(\mathbf{r}(t)=\left( \dfrac{1}{2}t^{2}+t\right) \mathbf{i}+t^{3}\mathbf{j}\) from \(t=0\) to \(t=2\).

(b) the space curve \(\mathbf{r}(t)=t\mathbf{i}+t^{2}\mathbf{j}+t^{3}\mathbf{k}\) from \(t=0\) to \(t=2.\)

For each curve, graph the motion of the particle and the vectors \(\mathbf{v}(1)\) and \(\mathbf{a}(1)\).

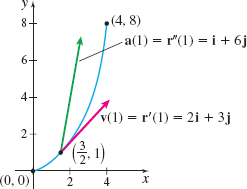
Solution (a) The velocity, acceleration, and speed are \begin{eqnarray*} \mathbf{v}(t)&\;=\;&\mathbf{r}^{\prime} (t)=\dfrac{d}{dt}\left( \dfrac{1}{2} t^{2}+t\right) \mathbf{i}+\dfrac{d}{dt}t^{3}\mathbf{j}=(t+1)\mathbf{i}+3t^{2} \mathbf{j} \\[6pt] \mathbf{a}(t)&\;=\;&\mathbf{r}^{\prime \prime} (t)=\dfrac{d}{dt}\mathbf{r^{\prime} } ( t)\;=\;\dfrac{d}{dt}(t+1)\mathbf{i}+\dfrac{d}{dt}3t^{2}\mathbf{j=i} +6t\mathbf{j} \\[6pt] v(t)&\;=\;&\left\Vert \mathbf{v}(t)\right\Vert\;=\;\sqrt{( t+1) ^{2}+( 3t^{2}) ^{2}}=\sqrt{9t^{4}+t^{2}+2t+1} \end{eqnarray*}

At \(t=1\), the velocity is \(\mathbf{v}(1)=\mathbf{r}^{\prime} (1)=2\mathbf{i}+3\mathbf{j}\) and the acceleration is \(\mathbf{a}(1)=\mathbf{r}^{\prime \prime}(1)=\mathbf{i}+6\mathbf{j}\). Figure 25 illustrates the graph of \(\mathbf{r}=\mathbf{r}( t)\), \(\mathbf{v}(1)\), and \(\mathbf{a}(1)\).

786

(b) The velocity, acceleration, and speed of the particle are \begin{eqnarray*} \mathbf{v}(t)&\;=\;&\mathbf{r}^{\prime} (t)=\dfrac{d}{dt}t\mathbf{i}+\dfrac{d}{dt} t^{2}\mathbf{j}+\dfrac{d}{dt}t^{3}\mathbf{k}=\mathbf{i}+2t\mathbf{j}+3t^{2} \mathbf{k} \\[12pt] \mathbf{a}(t)&\;=\;&\mathbf{r}^{\prime \prime} (t)=\dfrac{d}{dt}\mathbf{r^{\prime} } ( t)\;=\;\dfrac{d}{dt}\mathbf{i}+\dfrac{d}{dt}( 2t) \mathbf{j}+\dfrac{d}{dt}( 3t^{2}) \mathbf{k}=2\mathbf{j}+6t \mathbf{k} \\[12pt] v(t)&\;=\;&\left\Vert \mathbf{v}(t)\right\Vert\;=\;\sqrt{1^{2}+( 2t) ^{2}+( 3t^{2}) ^{2}}=\sqrt{1+4t^{2}+9t^{4}} \end{eqnarray*}

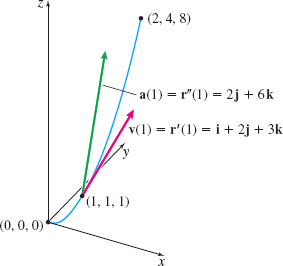
At \(t=1\), the velocity is \(\mathbf{v}(1)=\mathbf{i}+2\mathbf{j}+3\mathbf{k}\) and the acceleration is \(\mathbf{a}(1)=2\mathbf{j}+6\mathbf{k}\). See Figure 26.