The position of a particle of mass $m$ that is moving along an ellipse with a constant angular speed $\omega$ is given by the vector function $$\begin{equation*} \mathbf{r}(t)=A\cos ( \omega t) \mathbf{i}+B\sin ( \omega t) \mathbf{j}\qquad 0\leq t\leq 2\pi \end{equation*}$$

Find the force $\mathbf{F}$ acting on the particle at any time $t.$ Graph $\mathbf{r}=\mathbf{r}( t)$ and $\mathbf{F}=\mathbf{F}( t) .$

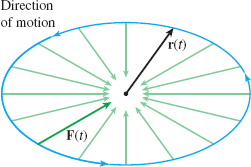
Figure 27 $\mathbf{F}(t)=-m\omega^2 \mathbf{r}(t)$

Solution To find the force $\mathbf{F}$, we use Newton's Second Law of Motion, $\mathbf{F}=m\mathbf{a}$. We begin by finding the acceleration $\mathbf{a}$ of the particle. $$\begin{eqnarray*} \mathbf{r}(t)&\;=\;&A\cos ( \omega t) \mathbf{i}+B\sin ( \omega t) \mathbf{j} \\[3pt] \mathbf{v}(t)&\;=\;&\mathbf{r^{\prime} }(t)=-A\omega \sin ( \omega t) \mathbf{i}+B\omega \cos ( \omega t) \mathbf{j} \\[3pt] \mathbf{a}(t)&\;=\;&\mathbf{r^{\prime \prime} }(t)=-A\omega ^{2}\cos ( \omega t) \mathbf{i}-B\omega ^{2}\sin ( \omega t) \mathbf{j} =-\omega ^{2}\mathbf{r}(t) \end{eqnarray*}$$

Then, by Newton's Law, $$\begin{equation*} \mathbf{F}(t)=m\mathbf{a}(t)=-m\hbox{ }\omega ^{2}\mathbf{r}(t) \end{equation*}$$

The direction of the force vector $\mathbf{F}$ is opposite to that of the vector $\mathbf{r}$ at any time $t$, as shown in Figure 27.