(a) Find the position $\mathbf{r}=\mathbf{r}( t)$ of a particle that moves counterclockwise along a circle of radius $R$ with a constant speed $v_{0}$.

(b) Find the velocity and acceleration of the particle.

(c) Find the magnitude of the acceleration.

Figure 28

Solution For convenience, we place the circle of radius $R$ in the $xy$-plane, with its center at the origin, and assume that at time $t=0$ the particle is on the positive $x$-axis.

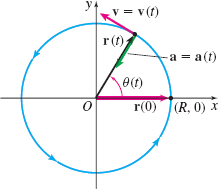
(a) The particle is moving counterclockwise along the circle, as shown in Figure 28. If $\theta (t)$ is the angle between the positive $x$-axis and the position vector of the particle $\mathbf{r}=$ $\mathbf{r}(t)$, then the vector $\mathbf{r=r}( t)$ is $$\begin{equation*} \mathbf{r}(t)=R \cos [\theta (t)]{\bf i}+R\;\sin [\theta (t)]{\bf j}\tag{1} \end{equation*}$$

787

Notice that $\mathbf{r}( 0)\;=\;R\mathbf{i}$, as required. Also for the motion to be counterclockwise, the function $\theta\;=\;\theta ( t)$ must be increasing.

(b) The velocity $\mathbf{v}$ of the particle is $$\begin{equation*} \mathbf{v}(t)=\frac{d\mathbf{r}}{dt}=-R\;\sin [\theta (t)]\frac{d\theta }{dt} \mathbf{i}+R\;\cos [\theta (t)]\frac{d\theta }{dt}\mathbf{j}\qquad \color{#0066A7}{\hbox{Use the Chain Rule.}} \end{equation*}$$

and the speed $v$ of the particle is $$\begin{eqnarray*} v(t)&=&\left\Vert \mathbf{v}(t)\right\Vert\;=\;\sqrt{R^{2}\sin ^{2}[\theta (t)]\left( \frac{ d\theta }{dt}\right) ^{2}+R^{2}\cos ^{2}[\theta (t)]\left( \frac{d\theta }{dt} \right) ^{2}}\\[6pt] &=&\sqrt{R^{2}\!\left( \frac{d\theta }{dt}\right) ^{2}}=R\left\vert \frac{d\theta }{dt}\right\vert \end{eqnarray*}$$

Since we know the speed is constant, $v(t)=v_{0}$. Also, since the function $\theta\;=\;\theta ( t)$ is increasing, $\dfrac{d\theta }{dt}>0$. As a result, $$\begin{eqnarray*} v_{0}&=&R\frac{d\theta }{dt} \\[4pt] \frac{d\theta }{dt}&=&\frac{v_{0}}{R} \end{eqnarray*}$$

Since $\dfrac{d\theta }{dt}$ is the rate at which the angle $\theta$ is changing, the quantity $\dfrac{v_{0}}{R}$ is the angular speed $\omega$ of the particle. That is, $$\begin{equation*} \frac{d\theta }{dt}=\omega \end{equation*}$$

We solve this differential equation, using $\theta ( 0)\;=\;0$ as the initial condition. $$\begin{eqnarray*} d\theta &=&\omega dt \\[3pt] \theta ( t) &=&\omega t+k \\[3pt] \theta ( 0) &=&k=0 \end{eqnarray*}$$

So, $\theta (t)=\omega t$. Now substitute $\theta (t)=\omega t$ into the vector function $\mathbf{r=r}( t)$ [statement (1)] to obtain $$\begin{equation*} \mathbf{r}(t)=R\;\cos ( \omega t) \mathbf{i}+R\;\sin ( \omega t) \mathbf{j} \end{equation*}$$

Then the velocity $\mathbf{v}$ and acceleration $\mathbf{a}$ of the particle are $$\begin{eqnarray*} \mathbf{v}\;=\;\mathbf{v}(t) &=& -R\omega \sin ( \omega t) \mathbf{i} +R\omega \cos ( \omega t) \mathbf{j} \\[3pt] \mathbf{a}\;=\;\mathbf{a}(t) &=& -R\omega ^{2}\cos ( \omega t) \mathbf{i }-R\omega ^{2}\sin ( \omega t) \mathbf{j}=-\omega ^{2}\left[ R\;\cos ( \omega t) \mathbf{i}+R\;\sin ( \omega t) \mathbf{ j}\right]\\[3pt] &=&-\omega ^{2}\mathbf{r}(t) \end{eqnarray*}$$

(c) Since $\omega=\dfrac{v_{0}}{R}$, the magnitude of the acceleration is $$\begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\left\Vert \mathbf{a}(t)\right\Vert\;=\;\omega ^{2}\left\Vert \mathbf{r}(t)\right\Vert\;=\;\omega ^{2}R=\dfrac{v_{0}^{2}}{R}}\tag{2} \end{equation*}$$