Finding the Tangential and Normal Components of Acceleration for an Elliptical Path

Find the tangential component \(a_{\mathbf{T}}\) and normal component \(a_{\mathbf{N}}\) of the acceleration of a particle moving along the ellipse \begin{equation*} \mathbf{r}(t)=3\sin t\mathbf{i}+4\cos t\mathbf{j}\quad 0\leq t\leq 2\pi \end{equation*}

Graph the ellipse, showing \(\mathbf{a}=\mathbf{a}( t), a_{\mathbf{T}}\), and \(a_{\mathbf{N}}\) when \(t=0,\) \(\dfrac{\pi }{4},\) and \( \dfrac{\pi }{2}\).

Solution We begin by finding the velocity, speed, and acceleration of the particle. \begin{eqnarray*} \mathbf{v}(t)&=&\mathbf{r}^{\prime} (t)=3\cos t\mathbf{i}-4\sin t\mathbf{j}\\[3pt] v(t)&=&\left\Vert \mathbf{v}(t)\right\Vert\;=\;\sqrt{(3\cos t)^{2}+(-4\sin t)^{2}}=\sqrt{9\cos ^{2}t+16\sin ^{2}t} \\[3pt] \mathbf{a}(t)&=&\mathbf{r}^{\prime \prime} (t)=-3\sin t\mathbf{i}-4\cos t \mathbf{j} \end{eqnarray*}

The tangential component of the acceleration is \begin{eqnarray*} a_{\mathbf{T}}=v^{\prime} ( t) &=&\dfrac{d}{dt}\sqrt{9\cos ^{2}t+16\sin ^{2}t}\\[3pt] &=&\dfrac{1}{2}( 9\cos ^{2}t+16\sin ^{2}t) ^{-1/2}[ 18\cos t ( -\!\sin t) +32\sin t (\cos t)]\\[3pt] &=&\frac{7\sin t\cos t}{\sqrt{9\cos ^{2}t+16\sin ^{2}t}} \end{eqnarray*}

To find the normal component of the acceleration, we need to find the curvature \(\kappa \) of \(\mathbf{r}=\mathbf{r}( t)\). \begin{eqnarray*} \kappa &=&\dfrac{\left\Vert \mathbf{r}^{\prime} ( t) \times \mathbf{r} ^{\prime \prime} ( t) \right\Vert }{\left\Vert \mathbf{r}^{\prime} ( t) \right\Vert ^{3}}=\dfrac{ \left|\begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] 3\cos t & -4\sin t & 0 \\[3pt] -3\sin t & -4\cos t & 0 \end{array}\right| }{( 9\cos ^{2}t+16\sin ^{2}t) ^{3/2}}=\dfrac{\left\vert\!-\!12\cos^{2}t-12\sin ^{2}t\right\vert }{( 9\cos ^{2}t+16\sin ^{2}t) ^{3/2} }\\[3pt] &=&\dfrac{12}{( 9\cos ^{2}t+16\sin ^{2}t) ^{3/2}} \end{eqnarray*}

Then \begin{equation*} a_{\mathbf{N}}=v^{2}( t) \kappa\;=\;( 9\cos ^{2}t+16\sin ^{2}t) \dfrac{12}{( 9\cos ^{2}t+16\sin ^{2}t) ^{3/2}}=\frac{ 12}{\sqrt{9\cos ^{2}t+16\sin ^{2}t}} \end{equation*}

The motion of the particle on the ellipse starts at \(\mathbf{r}(0)=4\mathbf{j}\). As \(t\) increases, \(x( t)\;=\;3 \sin t\) increases and \(y( t)\;=\;4\cos t\) decreases, so the motion of the particle is clockwise.

At \(t=0,\) \begin{equation*} \mathbf{a}( 0)\;=\;-3( 0) \mathbf{i}-4( 1) \mathbf{j}=-4\mathbf{j}\quad a_{\mathbf{T}}=\dfrac{7( 0) ( 1) }{3}=0\quad a_{\mathbf{N}}=\dfrac{12}{3}=4 \end{equation*}

At \(t=\dfrac{\pi }{4}\), \(\mathbf{r}\left( \dfrac{\pi }{4}\right)\;=\;\dfrac{3\sqrt{2}}{2}\mathbf{i}+2\sqrt{2}\mathbf{j}\), and \begin{equation*} \mathbf{a}\left( \dfrac{\pi }{4}\right)\;=\;-\dfrac{3\sqrt{2}}{2}\mathbf{i}-2 \sqrt{2}\mathbf{j}\quad a_{\mathbf{T}}=\dfrac{7\sqrt{2}}{10}\quad a_{\mathbf{N}}=\dfrac{12\sqrt{2}}{5} \end{equation*}

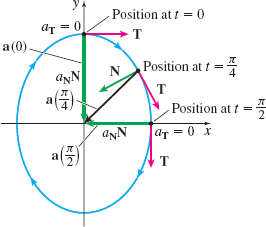
At \(t=\dfrac{\pi }{2}\), \(\mathbf{r}\left( \dfrac{\pi }{2}\right)\;=\;3\mathbf{i}+4( 0) \mathbf{j}=3\mathbf{i}\), and \begin{equation*} \mathbf{a}\left( \dfrac{\pi }{2}\right)\;=\;-3( 1) \mathbf{i} -4( 0) \mathbf{j=}-\!3\mathbf{i}\quad a_{\mathbf{T} }=0\quad a_{\mathbf{N}}=\dfrac{12}{4}=3 \end{equation*}

See Figure 30.