A car on the ramp of a multistory parking garage travels along a curve traced out by $\mathbf{r}( t)\;=\;10\cos t\mathbf{i}+10\sin t\mathbf{j}+3t\mathbf{k}$, where $t$ is the time in hours and distance is in miles. Find the tangential component $a_{\mathbf{T}}$ and normal component $a_{\mathbf{N}}$ of the acceleration of the car. What are the magnitude and direction of the force on the driver?

Solution We begin by finding the velocity $\mathbf{v}$, speed $v$, and acceleration $\mathbf{a}$ of the car. $$\begin{eqnarray*} \mathbf{v}(t)&\;=\;&\mathbf{r}^{\prime} (t)=\dfrac{d}{dt}( 10\cos t) \mathbf{i}+\dfrac{d}{dt}( 10\sin t) \mathbf{j}+\dfrac{d}{dt} ( 3t) \mathbf{k}=-10\sin t\mathbf{i}+10\cos t\mathbf{j+}3 \mathbf{k} \\[6pt] v(t)&\;=\;&\left\Vert \mathbf{v}(t)\right\Vert\;=\;\left\Vert \mathbf{r}^{\prime} (t)\right\Vert\;=\;\sqrt{(-10\sin t)^{2}+(10\cos t)^{2}+9}=\sqrt{109}\approx 10.440 \enspace \textrm{mi/h}\\[6pt] \mathbf{a}(t)&\;=\;&\mathbf{r^{\prime\prime}} (t)=\dfrac{d}{dt}\mathbf{v}(t)= -10\cos t\mathbf{i}-10\sin t\mathbf{j } \end{eqnarray*}$$

Since the speed is constant, the tangential component of acceleration $a_{ \mathbf{T}}$ is $$\begin{eqnarray*} a_{\mathbf{T}}=\dfrac{dv}{dt}=0 \end{eqnarray*}$$

The normal component of acceleration $a_{\mathbf{N}}$ is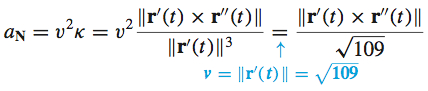

Since, $$\begin{equation*} \mathbf{r}^{\prime} (t)\times \mathbf{r}^{\prime \prime} (t)= \left|\begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] -10\sin t & 10\cos t & 3 \\[3pt] -10\cos t & -10\sin t & 0 \end{array}\right| =30\sin t\mathbf{i}-30\cos t\mathbf{j}+100\mathbf{k} \end{equation*}$$

the normal component is $$\begin{eqnarray*} a_{\mathbf{N}}&=&\frac{\left\Vert 30\sin t\mathbf{i}-30\cos t\mathbf{j}+100 \mathbf{k}\right\Vert }{\sqrt{109}}=\dfrac{\sqrt{900\sin ^{2}t+900\cos ^{2}t+10000} }{\sqrt{109}}\\[4pt] &=&\dfrac{\sqrt{10900}}{\sqrt{109}}=10 \end{eqnarray*}$$

As the car travels on the ramp at a constant speed, the force $$\mathbf{F}=m\mathbf{a}\;=\;ma_{\mathbf{N}} \mathbf{N}\;=\;10 m \mathbf{N}$$

pulls the car and driver toward the center of the ramp, with a magnitude about $10$ times the mass of the car.