Finding the Domain of a Function of Two Variables

Find the domain of each of the following functions. Then graph the domain.

1. \(z=f(x, y)=\sqrt{16-x^{2}-y^{2}}\)
2. \(z= f(x,y)=\ln (y^{2}-4x)\)

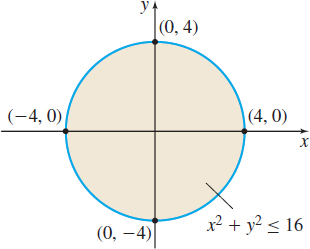
Solution (a) Since the expression under the radical must be nonnegative, the domain of \(f\) consists of all points in the plane for which \[ \begin{eqnarray*} 16-x^{2}-y^{2} &\geq &0 \\[4pt] x^{2}+y^{2} &\leq &16 \end{eqnarray*} \]

The domain is all the points inside and on the circle \(x^{2}+y^{2}=16\). The shaded portion of Figure 3 illustrates the domain.

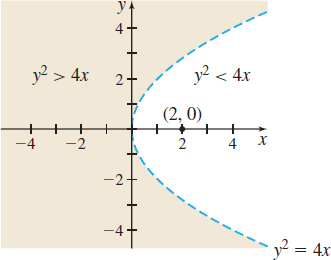
(b) Since the logarithmic function is defined for only positive numbers, the domain of \(f\) is the set of points \((x,y) \) for which \(y^{2}-4x>0\) or \(y^{2}>4x\). To graph the domain, we start with the parabola \(y^{2}=4x,\) and use a dashed curve to indicate that the parabola is not part of the domain. The parabola \(y^{2}=4x\) divides the plane into two sets of points: those for which \(y^{2}<4x\) and those for which \(y^{2}>4x\). To find which points are in the domain, choose any point not on the parabola \(y^{2}=4x\) and determine whether it satisfies the inequality. For example, the point \((2,0)\) is not in the domain, since \(0^{2}<(4)(2)\). The set of points for which \(y^{2}>4x\), the domain of \(f\), is shaded in Figure 4.