Graphing Level Curves

Graph the level curves of the function \(z=f(x, y)=x^{2}+4y^{2}+1\) for \(c = 1,2,5\), and \(17.\)

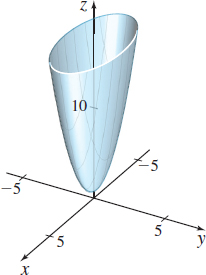
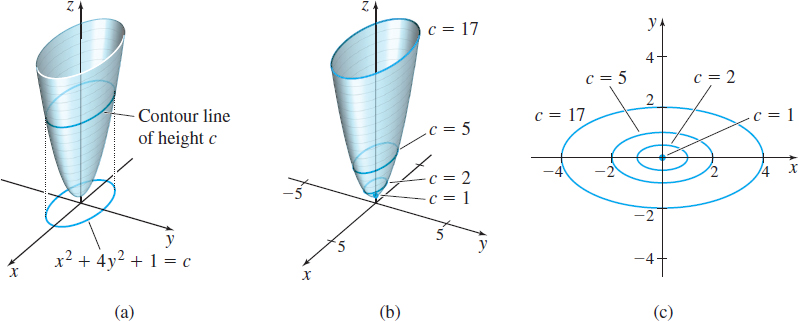
Solution  Here, we recognize the graph of \(f\) to be an elliptic paraboloid, as shown in Figure 12. Since \(z\geq 1,\) the level curves of \(f\) consist of the graphs of \(x^{2}+4y^{2}=c-1,\) \(c\geq 1.\) Figure 13(a) shows the elliptic paraboloid and a level curve \[ x^{2}+4y^{2}+1=c\qquad c>1 \]

Figure 13(b) shows the elliptic paraboloid \(\ z=x^{2}+4y^{2}+1\) with several contour lines marked. The level curves for \(c=1\) [the point \((0,0) \)], \(c=2, c=5\), and \(c=17\) are then graphed in Figure 13(c). Notice that the level curves are concentric ellipses. You should be able to see how the elliptic paraboloid evolves from the collection of its level curves.