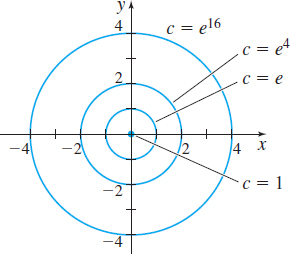
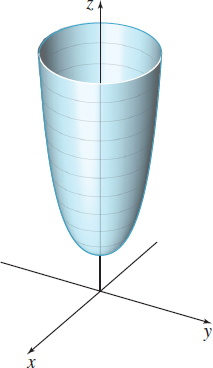
Graphing Level Curves

Graph the level curves of the function \(z=f(x,y)=e^{x^{2}+y^{2}}\) for \(c=1, e, e^{4},\) and \(e^{16}\).

Solution  Because \(x^{2}+y^{2}\geq 0,\) it follows that \(z\geq e^{0}=1\). The level curves satisfy the equation \(e^{x^{2}+y^{2}}=c\) or \( x^{2}+y^{2}=\ln c, \)where \(c\geq 1\). For \(c=1,\) the level curve is the point \((0,0)\). If \(c>1,\) the level curves are concentric circles. Figure 14 illustrates several level curves of \(f\). A graph of the surface \( z=e^{x^{2}+y^{2}}\) is given in Figure 15. Do you see how the graph evolved from the collection of its level curves?