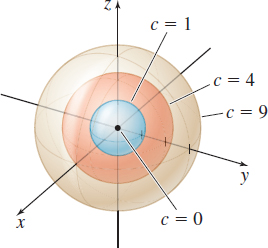
Figure 16 Level surfaces $x^{2} + y^{2} + z^{2} =c$.

Describe the level surfaces of the function $w=f(x,y,z)=x^{2}+y^{2}+z^{2}$.

Solution  Since $w\geq 0$, the level surfaces are the graphs of $$\begin{equation*} x^{2}+y^{2}+z^{2}=c\qquad c\geq 0 \end{equation*}$$

These are concentric spheres if $c>0$ and the origin if $c=0.$ See Figure 16.