Showing That a Limit Does Not Exist

Show that \(\lim\limits_{(x, y)\rightarrow (0, 0)}\dfrac{xy}{ x^{2}+y^{2}}\) does not exist.

Solution  Look at the denominator. Since \(\lim\limits_{(x, y) \rightarrow (0, 0)}( x^{2}+y^{2}) =0\), we cannot use the limit of a quotient to investigate the limit. We investigate the limit using two curves that contain \((0,0)\), say, \(y=2x\) and \(y=-x.\)

First we investigate the limit using the line \(y=2x\). Then \[ \begin{equation*} {\rm Using}\; y=2x: \quad \lim\limits_{(x, y)\rightarrow (0, 0)}\dfrac{x\left( 2x\right) }{x^{2}+\left( 2x\right) ^{2}}=\lim\limits_{x\rightarrow 0}\dfrac{ 2x^{2}}{x^{2}+4x^{2}}=\lim\limits_{x\rightarrow 0}\dfrac{2x^{2}}{5x^{2}}= \dfrac{2}{5} \end{equation*} \]

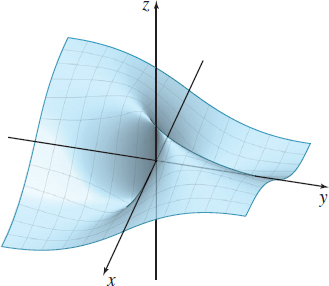
Now we investigate the limit using the line \(y=-x\). \[ \begin{equation*} {\rm Using}\; y=-x: \quad \lim\limits_{(x, y)\rightarrow (0, 0)}\dfrac{x\left( -x\right) }{x^{2}+\left( -x\right) ^{2}}=\lim\limits_{x\rightarrow 0}\dfrac{ -x^{2}}{x^{2}+x^{2}}=\lim\limits_{x\rightarrow 0}\dfrac{-x^{2}}{2x^{2}}=- \dfrac{1}{2} \end{equation*} \]

Since two different answers are obtained, the limit does not exist.