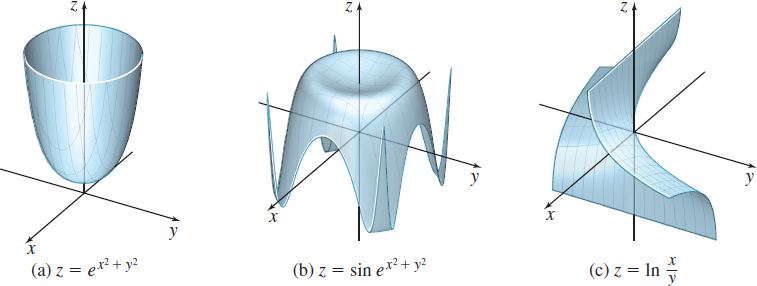
EXAMPLE 6Determining Where a Function Is Continuous
- (a) The function z=et is continuous for all t, and the function t=x2+y2 is continuous on its domain (all points in the plane), so the composite z=ex2+y2 is continuous on its domain (all points in the plane), as shown in Figure 29(a).
- (b) The sine function z=sint is continuous for all t, and the function t=ex2+y2 is continuous for all points (x,y) in the plane, so the composite z=sinex2+y2 is continuous for all points (x,y) in the plane, as shown in Figure 29(b).
- (c) The function z=lnt is continuous for all t>0, and the function t=yx is continuous for all x≠0. The composite function z=lnyx is continuous for all (x,y) for which x>0, y>0 or x<0, y<0. The graph of z has no points for which x≥0, y≤0 or x≤0, y≥0, as shown in Figure 29(c).