Finding Rates of Change

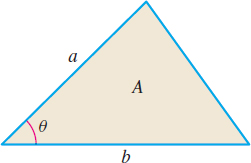
See Figure 35.

The area \(A\) of a triangle with sides \(a\) and \(b\) and included angle \(\theta \) is given by \[ A=\dfrac{1}{2}ab\;\sin\;\theta \]

1. Find the rate of change of \(A\) with respect to \(a\) when \(b\) and \(\theta\) are held fixed.
2. Find the rate of change of \(A\) with respect to \(b\) when \(a\) and \(\theta\) are held fixed.
3. Find the rate of change of \(A\) with respect to \(\theta\) when \(a\) and \(b\) are held fixed.
4. Evaluate each of the above if \(a=20\), \(b=30\), and \(\theta =\dfrac{\pi }{6}\).
5. Interpret the results found in (d).

Solution  (a) \(\dfrac{\partial A}{\partial a}=\dfrac{1}{2}b\;\sin \theta\) (b) \(\dfrac{\partial A}{\partial b}=\dfrac{1}{2} a\;\sin \theta\) (c) \(\dfrac{\partial A}{\partial \theta }=\dfrac{1}{2}ab\;\cos \theta\) (d) When \(a=20\), \(b=30\), and \(\theta =\dfrac{\pi }{6}\), then \[ \begin{eqnarray*} \dfrac{\partial A}{\partial a} &=&\dfrac{1}{2}(30)\;\left( \sin \frac{\pi }{6}\right) =\dfrac{15}{2} \\[4pt] \dfrac{\partial A}{\partial b} &=&\dfrac{1}{2}(20)\;\left( \sin \frac{\pi }{6}\right) =5 \\[4pt] \dfrac{\partial A}{\partial \theta } &=&\dfrac{1}{2}\left( 20\right) (30)\;\cos \dfrac{\pi }{6}=150\sqrt{3} \end{eqnarray*} \]

(e) Each partial derivative equals the rate of change of area with respect to \(a,\) \(b,\) or \(\theta\). The relative size of each rate of change tells us that the area will increase most rapidly when \(a\) and \(b\) are fixed and \(\theta\) varies. The area increases the least when \(a\) and \(\theta\) are fixed and \(b\) varies.