Showing That a Function of Two Variables Having Partial Derivatives Is Not Continuous

Show that the function \[ f(x, y)=\left\{ \begin{array}{@{}c@{\quad}c@{\quad}c} \dfrac{xy}{x^{2}+y^{2}} & \hbox{if} & (x,y)\neq (0,0) \\ 0 & \hbox{if} & (x,y)=(0,0) \end{array} \right. \]

has partial derivatives at \((0,0),\) but is not continuous at that point.

836

Solution We use the definition to find the partial derivatives of \(f\) at \((0,0)\).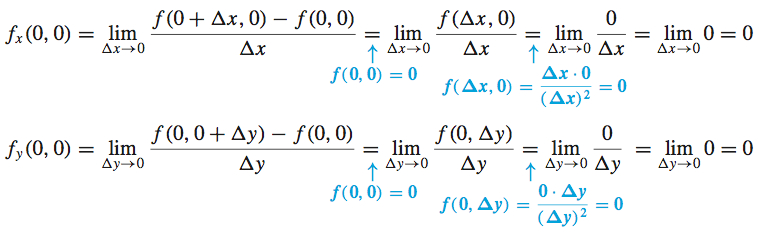

The partial derivatives \(f_{x}(0,0)\) and \(f_{y}(0,0)\) both exist.

But \(\lim\limits_{(x, y)\rightarrow (0, 0)}\dfrac{xy}{x^{2}+y^{2}}\) does not exist. (See Example 2 from Section 12.2.) As a result, \(f\) is not continuous at \((0,0)\).