Interpreting the Directional Derivative as a Slope

Find the directional derivative of \(f(x,y)=x\sin y\) at the point \(\left( 2, \dfrac{\pi }{3}\right)\) in the direction of \(\mathbf{a}=3\mathbf{i}+4 \mathbf{j}\). Interpret the result as a slope.

Solution To find a directional derivative of a function \(f\) in the direction of \(\mathbf{a}\), where \(\mathbf{a}\) is a nonzero vector, we must first find the unit vector in the direction of \(\mathbf{a}\). The unit vector \(\mathbf{u}\) in the direction of \(\mathbf{a}\) is \[ \begin{equation*} \mathbf{u}=\frac{\mathbf{a}}{\Vert \mathbf{a}\Vert }=\dfrac{3\mathbf{i}+4 \mathbf{j}}{\sqrt{9+16}}=\frac{3}{5}\mathbf{i}+\frac{4}{5}\mathbf{j} \end{equation*} \]

The partial derivatives of \(f\) \[ f_{x}(x,y)=\sin y\qquad \hbox{and}\qquad f_{y}(x,y)=x\cos y \]

are continuous throughout the plane, so \(f\) is differentiable. Using the unit vector \(\mathbf{u}=\dfrac{3}{5}\mathbf{i}+\dfrac{4}{5}\mathbf{j=}\cos \theta \mathbf{\mathbf{i}+}\sin \theta \mathbf{{j}}\), we find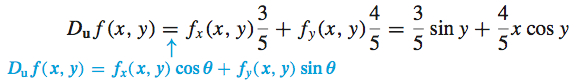

At the point \(\left( 2,\dfrac{\pi }{3}\right)\), \[ \begin{equation*} D_{\mathbf{u}}f\!\left( 2,\frac{\pi }{3}\right) =\dfrac{3}{5}\sin \dfrac{\pi }{3}+\dfrac{4}{5}\!\left( 2\cos \dfrac{\pi }{3}\right) =\dfrac{3}{5}\!\left( \frac{\sqrt{3}}{2}\right) +\dfrac{8}{5}\!\left(\dfrac{1}{2}\right)=\frac{3\sqrt{3}+8}{10} \end{equation*} \]

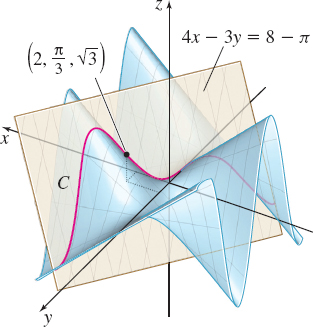
The slope of the tangent line to the curve \(C\) that is the intersection of the surface \(f( x,y) =x\sin y\) and the plane perpendicular to the \(xy\)-plane that contains the line through the point \(\left( 2,\dfrac{\pi }{3}, 0\right)\) in the direction \(\mathbf{a}\) is approximately 1.32. See Figure 4.