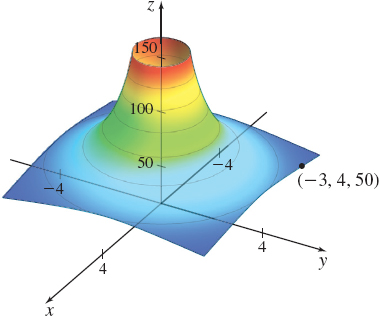
Modeling Temperature Change

A metal plate is placed on the \(xy\)-plane in such a way that the temperature \(T\) in degrees Celsius at any point \(P=(x,y)\) is inversely proportional to the distance of \(P\) from \((0,0)\). Suppose the temperature of the plate at the point \((-3,4)\) equals \({50^{\circ}{\rm C}}\).

1. Find \(T=T( x,y)\).
2. Find the gradient of \(T\) at the point \(( -3,4)\).
3. In what directions does the temperature increase most rapidly?
4. In what directions does the temperature decrease most rapidly?
5. In what directions is the rate of change of \(T\) at \((-3,4)\) equal to \(0\)?

869

Solution (a) The temperature \(T\) at any point \((x,y)\) is inversely proportional to the distance of \(( x,y)\) from the origin \((0,0)\). We can model \(T=T( x,y)\) as \[ T(x,y)=\dfrac{k}{\sqrt{x^{2}+y^{2}}} \]

where \(k\) is the constant of proportionality. Since \(T=50^{\circ}{\rm C}\) when \((x,y)=(-3,4)\), then \[ k=T\sqrt{x^{2}+y^{2}}=50\sqrt{( -3) ^{2}+4^{2}}=50(5)=250 \]

So, \(T=T( x,y) =\dfrac{250}{\sqrt{x^{2}+y^{2}}}\).

(b) The gradient of \(T=T( x,y) =\dfrac{250}{\sqrt{ x^{2}+y^{2}}}\) is \[ {\bf\nabla }T(x,y)=T_{x}(x,y)\mathbf{i}+T_{y}(x,y)\mathbf{j}=-\frac{250x }{(x^{2}+y^{2})^{3/2}}\mathbf{i}-\frac{250y}{(x^{2}+y^{2})^{3/2}}\mathbf{ j} \]

At \(( -3,4)\), \[ {\bf\nabla }T(-3,4)=-\frac{250 ( -3) }{ [ ( -3) ^{2}+4^{2}] ^{3/2}}\mathbf{i}-\frac{250 ( 4) }{ [ ( -3) ^{2}+4^{2}] ^{3/2}}\mathbf{j}=\frac{750}{125} \mathbf{i}-\frac{1000}{125}\mathbf{j}=6\mathbf{i}-8\mathbf{j} \]

(c) The temperature increases most rapidly in the direction \({\bf\nabla} T(-3,4)=6\mathbf{i}-8\mathbf{j}\).

(d) The temperature decreases most rapidly in the direction \(-{\bf\nabla }T(-3,4)=-6\mathbf{i}+8\mathbf{j}\).

(e) The rate of change in \(T\) at \((-3,4)\) equals \(0\) for directions orthogonal to \({\bf\nabla} T(-3,4)=6\mathbf{i}-8\mathbf{j}\). That is, the rate of change in \(T\) is \(0\) in either of the two directions orthogonal to \(6\mathbf{i}-8\mathbf{j}\), namely \(\pm ( 8\mathbf{i}+6 \mathbf{j})\).