Using the Second Partial Derivative Test

Find all local maxima, local minima, and saddle points for \[ z=f(x,y)=x^{3}+y^{2}+2xy-4x-3y+5 \]

Solution  The critical points are the solutions of the system of equations \[ \left\{ \begin{array}{rcll} f_{x}(x,y)&=&3x^{2}+2y-4&=0 \\[3pt] f_{y}(x,y)&=&2y+2x-3&=0 \end{array}\right. \]

We solve the system using substitution. Solving for \(y\) in \(f_{y}(x,y)=0\), we obtain \(y=\dfrac{1}{2}(3-2x)\). Then if we substitute for \(y\) in \( f_{x}(x,y)=0\), the result is \[ \begin{eqnarray*} 3x^{2}+2\,\left[ \dfrac{1}{2}(3-2x)\right] -4& =0 \\[4pt] 3x^{2}-2x-1& =0 \\[4pt] (3x+1)(x-1)& =0 \\[4pt] x=-\dfrac{1}{3}\qquad \hbox{or }\qquad x& =1 \end{eqnarray*} \]

883

When \(x=-\dfrac{1}{3}\), then \(y=\dfrac{1}{2}(3-2x)=\dfrac{1}{2}\left( 3+ \dfrac{2}{3}\right) =\dfrac{11}{6}\).

When \(x=1\), then \(y=\dfrac{1}{2}(3-2x)=\dfrac{1}{2}\).

The critical points are \(\left( -\dfrac{1}{3},\dfrac{11}{6}\right)\) and \( \left( 1,\dfrac{1}{2}\right) \).

The second-order partial derivatives of \(f\) are \[ f_{xx}(x,y)=6x\qquad f_{xy}(x,y)=2\qquad f_{yy}(x,y)=2 \]

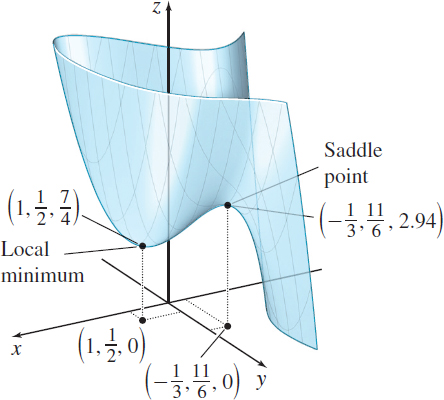
The function \(f\) satisfies the requirements of the Second Partial Derivative test at each critical point. At \(\left( -\dfrac{1}{3},\dfrac{11}{6}\right) \), \[ \begin{eqnarray*} &A=f_{xx}\left( -\dfrac{1}{3},\dfrac{11}{6}\right) =-2\qquad B=f_{xy}\left( -\dfrac{1}{3},\dfrac{11}{6}\right) =2\qquad C=f_{yy}\left( -\dfrac{1}{3},\dfrac{11}{6}\right) =2&\\[4pt] &AC-B^{2}=-4-4=-8<0& \end{eqnarray*} \]

So, \(\left( -\dfrac{1}{3},\dfrac{11}{6},\dfrac{317}{108}\right)\) is a saddle point of \(f\). At \(\left( 1,\dfrac{1}{2}\right) \), \[ A=f_{xx}\left( 1,\dfrac{1}{2}\right) =6\qquad B=f_{xy}\left( 1,\dfrac{1}{2}\right) =2\qquad C=f_{yy}\left( 1,\dfrac{1}{2}\right)=2 \]

Since \(AC-B^{2}=8>0\), \(f\) has a local minimum at \(\left( 1,\dfrac{1}{2}\right) \), where \(f\left( 1,\dfrac{1}{2}\right) =\dfrac{7}{4}\)