EXAMPLE 5Finding Absolute Extrema
Find the absolute maximum and the absolute minimum of z=f(x,y)=2x−2xy+y2
whose domain is the region defined by 0≤x≤4 and 0≤y≤3.
Solution The function f is continuous on its domain, which is a closed, bounded set. Then the Extreme Value Theorem guarantees that f has an absolute maximum and an absolute minimum on its domain. To find them, we first find the critical points of f, namely the solutions of the system of equations {fx(x,y)=2−2y=0fy(x,y)=−2x+2y=0
Solving the system of equations, we find that the only critical point is (1,1). The value of f at (1,1) is f(1,1)=2(1)−2(1)(1)+12=1
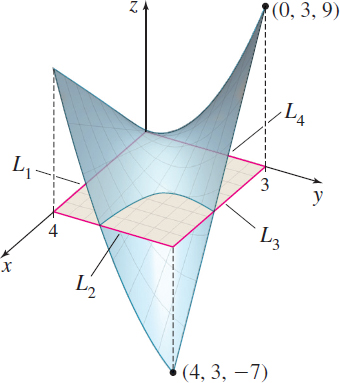
The domain of f is the set 0≤x≤4, 0≤y≤3. The boundary of the domain of f consists of the four line segments L1, L2, L3, and L4 shown in Figure 18. We evaluate f on each line segment.
On \boldsymbol L_{\bf 1}: x is in the interval \left[ 0,4\right] and y=0. The function f(x,y)=f(x,0)=2x is increasing on 0\leq x\leq 4, so its extreme values occur at the endpoints 0 and 4. \hbox{At }x=0, f(0,0)=0\qquad \hbox{and} \qquad \hbox{at}\ x=4, f(4,0)=8
On \boldsymbol L_{\bf 2}: x=4 and y is in the interval [0,3] . The function f(x,y)=f(4,y)= 8-8y+y^{2}. To find the extreme values of f on [0,3] , we begin by finding the critical number(s) of the function g(y) =8-8y+y^{2}. That is, we find where g' (y) =0. \begin{eqnarray*} g' (y) &=&-8+2y=0 \\[3pt] y &=&4 \end{eqnarray*}
Since 4 is not in the interval [0,3] , the extreme values occur at the endpoints 0 and 3. \hbox{At }y=0\hbox{, }\ f(4,0)=8\qquad \hbox{and} \qquad \hbox{at}y=3,\hbox{ }f(4,3)=-7
On \boldsymbol L_{\bf 3}: x is in the interval [ 0,4] and y=3. The function f(x,y)=f(x,3)= 2x-6x+9=-4x+9 is decreasing on 0\leq x\leq 4, so its extreme values occur at the endpoints 0 and 4. \hbox{At }x=0, f(0,3)=9\qquad \hbox{and} \qquad \hbox{at }x=4, f(4,3)=-7
On \boldsymbol L_{\bf 4}: x=0 and y is in the interval [0,3] . The function f(x,y)=f(0,y)=y^{2} is increasing on 0\leq y\leq 3, so its extreme values occur at the endpoints 0 and 3. \hbox{At }y=0, f(0,0)=0\qquad\hbox {and}\qquad \hbox{at }y=3,\hbox{ }f(0,3)=9
885
The values of f at the critical point (1,1) and at the extreme values on the boundary are
| Point | (1,1) | ( 0,0) | ( 4,0) | ( 4,3) | ( 0,3) |
| Value | 1 | 0 | 8 | -7 | 9 |
The absolute maximum value of f is f(0,3)=9; the absolute minimum value is f(4,3)=-7.