Using Lagrange Multipliers with Two Constraints
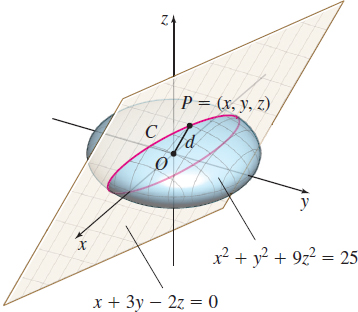
Find the points of intersection of the ellipsoid \(x^{2}+y^{2}+9z^{2}=25\) and the plane \(x+3y-2z=0\) that are farthest from the origin. Also find the points that are closest to the origin.
Let \(C\) be the curve formed by intersecting the ellipsoid and the plane, and let \(P=(x,y,z)\) be a point on \(C\). We use the steps for Lagrange multipliers.
Step 1 The function to be optimized is the distance \(d\) from \(P\) to the origin: \[ d=f(x,y,z)=\sqrt{x^{2}+y^{2}+z^{2}} \]
subject to the constraints \[ \begin{eqnarray*} g(x,y,z) &=&x^{2}+y^{2}+9z^{2}-25=0 \qquad \enspace \enspace {\color{#0066A7}{\hbox{The point must be on the ellipsoid.}}}\\ h(x,y,z) &=&x+3y-2z=0 \qquad \qquad \qquad {\color{#0066A7}{\hbox{The point must be on the plane.}}} \end{eqnarray*} \]
Step 2 The functions \(f,\) \(g,\) and \(h\) are each functions of three variables, and each has continuous partial derivatives at every point of some open set containing the smooth curve defined by \(g(x,y,z)=0\) and \(h(x,y,z)=0.\)
Step 3 We introduce two Lagrange multipliers and solve the system of equations \({\nabla }f(x,y,z)=\lambda _{1}{\nabla }g(x,y,z)+\lambda _{2}{\nabla }h(x,y,z)\), \(g(x,y,z)=0,\) and \(h(x,y,z)=0.\)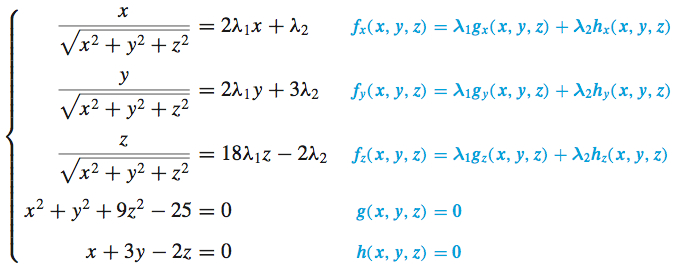
Eliminating \(\lambda _{1}\) and \(\lambda _{2}\) from the first three equations, we have two possibilities: \(z=0\) or \(y=3x\). Using each of these equations with the constraints
897
\(x^{2}+y^{2}+9z^{2}- 25=0\) and \(x+3y-2z=0\) results in the following: \[ \begin{eqnarray*} z&=&0{:} & \left( -\dfrac{15}{\sqrt{10}},\dfrac{5}{\sqrt{10}},0\right) \qquad \qquad \enspace \enspace \enspace {\color{#0066A7}{\hbox{5 units from the origin}}}\\ &&& \left( \dfrac{15}{\sqrt{10}},-\dfrac{5}{\sqrt{10}},0\right) \qquad \qquad \enspace \enspace \enspace {\color{#0066A7}{\hbox{5 units from the origin}}}\\ y&=&3x{:} & \left( \dfrac{5}{\sqrt{235}},\dfrac{15}{\sqrt{235}},\dfrac{25}{\sqrt{235}}\right) \qquad \enspace {\color{#0066A7}{\hbox{\(\sqrt{\dfrac{875}{235}}\approx 1.930\) units from the origin}}}\\ &&& \left( -\dfrac{5}{\sqrt{235}},-\dfrac{15}{\sqrt{235}},-\dfrac{25}{\sqrt{235}}\right) \enspace \enspace {\color{#0066A7}{\hbox{\(\sqrt{\dfrac{875}{235}}\approx\) 1.930 units from the origin}}} \end{eqnarray*} \]
The points \(\left( -\dfrac{15}{\sqrt{10}},\dfrac{5}{\sqrt{10}},0\right)\) and \(\left( \dfrac{15}{\sqrt{10}},-\dfrac{5}{\sqrt{10}},0\right)\) are farthest from the origin, and the points \(\left( \dfrac{5}{\sqrt{235}},\dfrac{15}{\sqrt{235}},\dfrac{25}{\sqrt{235}}\right)\) and \(\left( -\dfrac{5}{\sqrt{235}},-\dfrac{15}{\sqrt{235}},-\dfrac{25}{\sqrt{235}}\right)\) are closest to the origin. Since the intersection of the ellipsoid and the plane is an ellipse, the points we have found are the endpoints of the major and minor axes of this ellipse.