Find the surface area of the part of the surface $z=f(x, y)=\dfrac{2}{3} (x^{3/2}+y^{3/2})$ that lies above the region $R,$ a rectangle enclosed by the lines $x=0$, $x=1$, $y=0$, and $y=2$.

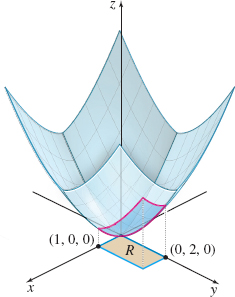
Figure 38 $z=\dfrac{2}{3}( x^{3/2}+y^{3/2})$

Solution Figure 38 shows the surface $z=f(x, y)=\dfrac{2}{3} (x^{3/2}+y^{3/2})$ and the surface area $S$ above the rectangle $R$. We begin by finding the partial derivatives of $z=f(x, y)$: $$f_{x}(x,y)=x^{1/2} \qquad f_{y}(x,y)=y^{1/2}$$

Since $f_x$ and $f_y$ are continuous on $R$, the surface area $S$ above $R$ is $$\begin{eqnarray*} S &=&\displaystyle\iint\limits_{\kern-3ptR}\sqrt{[f_{x}(x, y)]^{2}+[f_{y}(x,y)]^{2}+1} \,{\it dA}=\displaystyle\iint\limits_{\kern-3ptR}\sqrt{( x^{1/2}) ^{2}+( y^{1/2}) ^{2}+1}\,{\it dA} \notag \\ &=& \int_{0}^{1}\int_{0}^{2}\sqrt{x+y+1}\,{\it dy}\,{\it dx}=\int_{0}^{1}\left[ \dfrac{2}{3 }(x+y+1)^{3/2}\right] _{0}^{2}\,{\it dx} \notag \\ &=&\dfrac{2}{3}\int_{0}^{1}\big[ (x+3)^{3/2}-(x+1)^{3/2}\big] \,{\it dx}=\left( \dfrac{2}{3}\right) \left( \dfrac{2}{5}\right) \big[ (x+3)^{5/2}-(x+1)^{5/2}\big] _{0}^{1} \notag \\ &=&\dfrac{4}{15}( 32-9\sqrt{3}-4\sqrt{2}+1) = \dfrac{4}{15} (33-9\sqrt{3}-4\sqrt{2}) \end{eqnarray*}$$