Find the surface area of the part of the sphere $x^{2}+y^{2}+z^{2}=a^{2}$ that lies above the $xy$-plane and is contained within the cylinder $x^{2}+y^{2}=ax,$ $a\gt 0$.

Figure 40 $x^{2}+y^{2}+z^{2}=a^{2},$ $z\geq 0$

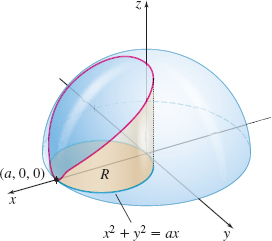
Solution Figure 40 shows the sphere and the cylinder. The equation of the surface in explicit form is $$z=f(x,y)=\sqrt{a^{2}-x^{2}-y^{2}}$$

The partial derivatives of $z$ $=f(x,y)$ are $$f_{x}(x,y)=-\dfrac{x}{\sqrt{a^{2}-x^{2}-y^{2}}}\qquad f_{y}(x,y)=- \dfrac{y}{\sqrt{a^{2}-x^{2}-y^{2}}}$$

The projection of the cylinder onto the $xy$-plane is the region $R$ enclosed by the circle $x^{2}+y^{2}=ax$, $a\gt 0.$ Then the surface area $S$ that we seek is $$S=\displaystyle\iint\limits_{\kern-3ptR}\sqrt{\dfrac{x^{2}}{a^{2}-x^{2}-y^{2}}+\dfrac{y^{2}}{ a^{2}-x^{2}-y^{2}}+1}\,\,{\it dA}=\displaystyle\iint\limits_{\kern-3ptR}\sqrt{\dfrac{a^{2}}{ a^{2}-x^{2}-y^{2}}}\,{\it dA}$$

Since the integrand involves the expression $x^{2}+y^{2}$ and the boundary of $R$ is the circle $x^{2}+y^{2}=ax$, we use polar coordinates $(r,\theta)$. We begin by finding the limits of integration. Since $$\begin{eqnarray*} x^{2}+y^{2} &=&ax \\ r^{2} &=&ar\cos \theta \\ r &=&a\cos \theta \end{eqnarray*}$$

we find that $r$ varies from $0$ to $a\cos \theta$.

Since half the area is to the right of the $xz$-plane and half is to the left of the plane, we can let $\theta$ vary from $0$ to $\dfrac{\pi }{2}$ and double the area. Then the surface area $S$ is $$\begin{array}{rcl} S& =&\int\limits\int_{\kern-11ptR}\sqrt{\dfrac{a^{2}}{a^{2}-x^{2}-y^{2}}}\,d\!A \underset{\underset{{\color{#0066A7}{\hbox {a>0}}}}{\color{#0066A7}{\uparrow }}}{=} \int\limits\int_{\kern-11ptR}\dfrac{a}{\sqrt{a^{2}-r^{2}}} \,r\,dr\,d\theta \underset{\underset{{\color{#0066A7}{\hbox{Double the area}}}}{\color{#0066A7}{\uparrow}}}{=} 2\int_{0}^{\pi /2}\!\!\int_{0}^{a\cos \theta }\dfrac{a}{\sqrt{a^{2}-r^{2}}} \,r\,dr\,d\theta \notag \\ \quad \\ &=&-2a\int_{0}^{\pi /2}\Big[ \sqrt{a^{2}-r^{2}}\Big] _{0}^{a\cos \theta }d\theta =-2a\int_{0}^{\pi /2}(a\sin \theta -a)\,d\theta\\ &=&-2a^{2}\big[-\cos \theta -\theta \big] _{0}^{\pi /2}=a^{2}(\pi -2) \end{array}$$