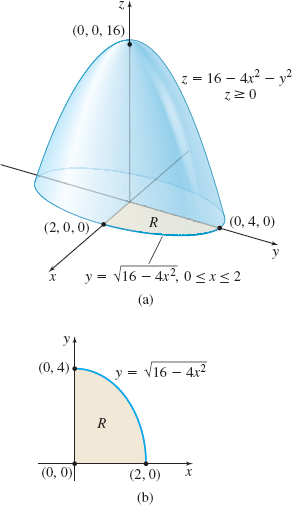
Finding the Volume of a Solid

Find the volume \(V\) of the solid \(E\) in the first octant that is enclosed by the paraboloid \(z=16-4x^{2}-y^{2}\) and the \(xy\)-plane.

Solution Figure 45(a) shows the solid \(E\), which is \(xy\)-simple. The upper surface is the paraboloid \(z=z_{2}(x, y)=16-4x^{2}-y^{2}\) and the lower surface is the plane \(z=z_{1}(x, y)=0\). The region \(R\) in the \(xy\)-plane is enclosed by the \(x\)-axis, the \(y\)-axis, and part of the ellipse \(4x^{2}+y^{2}=16,\) \(x\geq 0,\) \(y\geq 0.\)The region \(R\) is both \(x\)-simple and \(y\)-simple. We choose to use the iterated integral for an \(x\)-simple region, so that \(0\leq y\leq \sqrt{16-4x^{2}}\) and \(0\leq x\leq 2.\) See Figure 45(b). The volume \(V\) of \(E\) is given by \begin{eqnarray*} V&=&\iiint\limits_{\kern-2ptE}\,{\it dV}=\int_{a}^{b}\int_{y_{1}(x)}^{y_{2}(x)} \int_{z_{1}(x, y)}^{z_{2}(x, y)}{\it dz}\, {\it dy}\,{\it dx}= \int_{0}^{2} \int_{0}^{\sqrt{16-4x^{2}} } \int_{0}^{16-4x^{2}-y^{2}}{\it dz}\, {\it dy}\,{\it dx} \\[4pt] &=&\int_{0}^{2}\int_{0}^{\sqrt{16-4x^{2}}}( 16-4x^{2}-y^{2}) \,{\it dy}\,{\it dx}=\int_{0}^{2}\left[ (16-4x^{2})y-\dfrac{y^{3}}{3}\right] _{0}^{\sqrt{ 16-4x^{2}}}\,{\it dx} \\[4pt] &=&\int_{0}^{2}\!\left( (16-4x^2)^{3/2} -\dfrac{( 16-4x^{2}) ^{3/2}}{3}\right)\!{\it dx} = \dfrac{16}{3}\int^2_0 (4-x^2)^{3/2}\,{\it dx} \end{eqnarray*}

We use the Table of Integrals, Integral 69 with \(a=2\). Then \begin{eqnarray*} V=\dfrac{16}{3}\int^2_0 (4-x^2)^{3/2}\,{\it dx} &=&\dfrac{16}{3}\left[ \dfrac{x}{4} ( 4-x^{2}) ^{3/2}+\dfrac{3x}{2 }\sqrt{4-x^{2}}+6\sin ^{-1}\dfrac{x}{2}\right] _{0}^{2}\\[4pt] &=& \dfrac{16}{3} (6) \left(\dfrac{\pi}{2}\right)=16\pi \end{eqnarray*}