Finding the Mass and Center of Mass of a Solid

1. Find the mass \(M\) of a solid in the shape of a tetrahedron cut from the first octant by the plane \(x+y+z=1\) if the mass density \(\rho =\rho (x, y, z) \) is proportional to the distance from the \(yz\)-plane.
2. Find the center of mass \((\bar{x}, \bar{y}, \bar{z})\) of the tetrahedron.

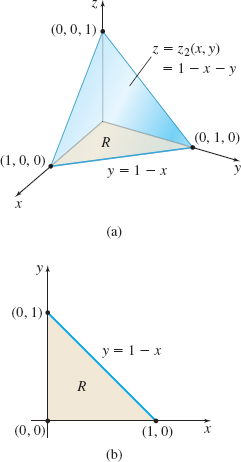
Solution Figure 46(a) shows the solid \(E\) that is \(xy\)-simple. It is enclosed by the surfaces \(z=z_{1}(x, y)=0\) and \(z=z_{2}(x, y)=1-x-y\), and its projection onto the \(xy\)-plane is the closed, bounded \(x\)-simple region \(R\) defined by the lines \(y=0\) and \(y=1-x,\) where \(0\leq x\leq 1\). See Figure 46(b).

(a) Since the mass density \(\rho =\rho (x, y,z) \) is proportional to the distance from the \(yz\)-plane, we have \(\rho (x, y,z) =kx,\) where \(k\) is the constant of proportionality. Then the mass \(M\) is \[ M=\iiint\limits_{\kern-2ptE}\rho (x, y, z) \,{\it dV}=\iiint\limits_{\kern-2ptE}kx\,{\it dV}=k\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-x-y}x \,{\it dz}\,{\it dy}\,{\it dx} \]

Using a CAS, \(M=\dfrac{k}{24}.\)

(b) The center of mass \((\bar{x}, \bar{y}, \bar{z})\) is \begin{eqnarray*} \bar{x}&=&\dfrac{\iiint\limits_{\kern-2ptE}x\rho ( x, y,z) \,{\it dV}}{M}=\dfrac{ \iiint\limits_{\kern-2ptE}xkx\,{\it dV}}{\dfrac{k}{24}}=24\iiint\limits_{\kern-2ptE}x^{2}\,{\it dV}\\[7pt] &=&24\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-x-y}x^{2}\,{\it dz}\,{\it dy}\,{\it dx} \end{eqnarray*}

Using a CAS, \(\overline{x}=\dfrac{2}{5}.\) \begin{equation*} \bar{y}=\dfrac{\iiint\limits_{\kern-2ptE}y\rho (x, y,z) \,{\it dV}}{M}=\dfrac{ \iiint\limits_{\kern-2ptE}ykx\,{\it dV}}{\dfrac{k}{24}}=24\int_{0}^{1}\int_{0}^{1-x} \int_{0}^{1-x-y}{\it xy}\,{\it dz}\,{\it dy}\,{\it dx} \end{equation*}

Using a CAS, \(\bar{y}=\) \(\dfrac{1}{5}.\)

946

\begin{equation*} \bar{z}=\dfrac{\iiint\limits_{\kern-2ptE}z\rho (x, y,z) \,{\it dV}}{M}=\dfrac{ \iiint\limits_{\kern-2ptE}zkx\,{\it dV}}{\dfrac{k}{24}}=24\int_{0}^{1}\int_{0}^{1-x} \int_{0}^{1-x-y}xz\,{\it dz}\,{\it dy}\,{\it dx} \end{equation*}

Using a CAS \(\ \bar{z}=\) \(\dfrac{1}{5}.\)

The center of mass of the tetrahedron is located at the point \(\left( \dfrac{2}{5},\dfrac{1}{5},\dfrac{1}{5}\right).\)