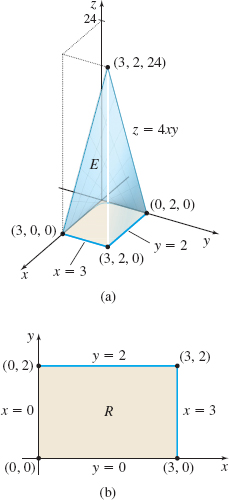
Finding the Moment of Inertia About the \(z\)-axis of a Solid
Find the moment of inertia about the \(z\)-axis of the homogeneous solid of mass density \(\rho \) in the first octant enclosed by the surface \(z=4xy\) and the planes \(z=0\), \(x=3\), and \(y=2\).
where \(r=\sqrt{x^{2}+y^{2}}\) is the distance of the point \((x, y, z) \) from the \(z\)-axis.
Figure 47(a) shows the solid \(E\), which is \(xy\)-simple. The upper surface is \(z=z_{2}(x, y)=4xy\) and the lower surface is the plane \(z=z_{1}(x, y)=0\). The region \(R\) in the \(xy\)-plane is enclosed by the \(x\)-axis, the \(y\)-axis, the line \(x=3\), and the line \(y=2\), as shown in Figure 47(b). The region \(R\) is both \(x\)-simple and \(y\)-simple. \begin{eqnarray*} I_{z} &=&\iiint\limits_{\kern-2ptE}(x^{2}+y^{2})\rho \,{\it dV}=\rho \int_{0}^{3}\int_{0}^{2}\int_{0}^{4xy}(x^{2}+y^{2})\,{\it dz}\,{\it dy}\,{\it dx} \notag \\[4pt] &=&\rho \int_{0}^{3}\int_{0}^{2}\big[ z(x^{2}+y^{2})\big] _{0}^{4xy}\,{\it dy}\,{\it dx}=\rho \int_{0}^{3}\int_{0}^{2}( 4x^{3}y+4xy^{3}) \,{\it dy}\,{\it dx}\\[4pt] &=&\rho \int_{0}^{3}\big[ 2x^{3}y^{2}+xy^{4}\big] _{0}^{2}\,\,{\it dx} \notag \\[4pt] &=&\rho \int_{0}^{3}( 8x^{3}+16x) \,{\it dx}=\rho \big[ 2x^{4}+8x^{2}\big] _{0}^{3}=\rho ( 162+72) =234\rho \end{eqnarray*}