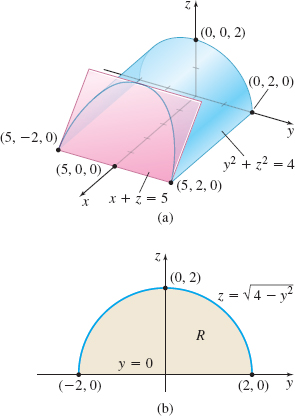
Finding the Volume of a Solid That Is \(yz\)-simple

Find the volume \(V\) of the solid \(E\) that is enclosed by the cylinder \(y^{2}+z^{2}=4,\) and the planes \(x=0,\) \(z=0,\) and \(x+z=5.\)

Solution Figure 50(a) shows that the solid \(E\) is \(yz\)-simple. The front surface is the plane \(x_{2}(y, z) =5-z\) and the back surface is the plane \(x_{1}(y, z) =0.\) The region \(R\) in the \(yz\)-plane is enclosed by the \(y\)-axis and the semi-circle \(z=\sqrt{4-y^{2}};\) it is \(y\)-simple. So, \(0\leq z\leq \sqrt{4-y^{2}}\) and \(-2\leq y\leq 2.\) See Figure 50(b). The volume \(V\) of \(E\) is given by \begin{eqnarray*} V &=&\iiint\limits_{\kern-2ptE}\,{\it dV}=\iint\limits_{\kern-2ptR}\left[ \int_{x_{1}(y,z)}^{x_{2}(y,z)}{\it dx}\right] {\it dz}\,{\it dy}=\int_{-2}^{2}\int_{0}^{ \sqrt{4-y^{2}}}\int_{0}^{5-z}{\it dx}\,{\it dz}\,{\it dy}\\[4pt] &=&\int_{-2}^{2}\int_{0}^{\sqrt{4-y^{2}} }( 5-z) \,{\it dz}\,{\it dy} =\int_{-2}^{2}\left[ 5z-\dfrac{z^{2}}{2}\right] _{0}^{\sqrt{4-y^{2}}}\,{\it dy}\\[4pt] &=&\int_{-2}^{2}\left( 5\sqrt{4-y^{2}}-\dfrac{4-y^{2}}{2}\right){\it dy}\\[4pt] &=&5\int_{-2}^{2}\sqrt{4-y^{2}}\, {\it dy}-\int_{-2}^{2}\left( 2-\dfrac{y^{2}}{2} \right) {\it dy} \notag \\[4pt] &=&5(2\pi) -\left[ 2y-\dfrac{y^{3}}{6}\right] _{-2}^{2}=10\pi -\dfrac{16}{3} \end{eqnarray*}