Give a geometric interpretation of the triple integral $$\begin{equation*} \int_{-1}^{1}\int_{-\sqrt{1-x^{2}}}^{\sqrt{1-x^{2}}}\int_{0}^{2\sqrt{ 1-x^{2}-y^{2}}}\,{\it dz}\,{\it dy}\,{\it dx} \end{equation*}$$

Then use cylindrical coordinates to find the triple integral.

Figure 55

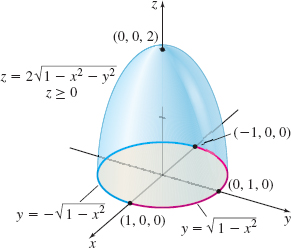
Solution The solid $E$ of integration and its projection onto the $xy$-plane can be described by the inequalities $$\begin{equation*} 0\leq z\leq 2\sqrt{1-x^{2}-y^{2}}\qquad -\sqrt{1-x^{2}}\leq y\leq \sqrt{1-x^{2}} \qquad -1\leq x\leq 1 \end{equation*}$$

The limits of integration on $z$ are $z=0$ and $z=2\sqrt{1-x^{2}-y^{2}}= \sqrt{4-4x^{2}-4y^{2}}$ or, equivalently, $z^{2}=4-4x^{2}-4y^{2},$ $z\geq 0.$ We can interpret the integral as the volume of a solid $E$ that is the upper half of the ellipsoid $4x^{2}+4y^{2}+z^{2}=4,$ $z\geq 0,$ as shown in Figure 55. From the $x$ and $y$ limits of integration, the projection onto the $xy$-plane is the region $R$ enclosed by the circle $x^{2}+y^{2}=1$.

To find the integral, we convert the rectangular coordinates to cylindrical coordinates. Then $$z=2\sqrt{1-x^{2}-y^{2}}=2\sqrt{1-(x^{2}+y^{2}) }=2\sqrt{1-r^{2}}$$

The projection onto the $xy$-plane is the region enclosed by the circle $x^{2}+y^{2}=1.$ So in cylindrical coordinates, we have $$0\leq z\leq 2\sqrt{1-r^{2}} \qquad 0\leq r\leq 1\qquad 0\leq \theta \leq 2\pi$$

Then $$\begin{array}{lll} \int_{-1}^{1}\int_{-\sqrt{1-x^{2}}}^{\sqrt{1-x^{2}}}\int_{0}^{2\sqrt{ 1-x^{2}-y^{2}}}\,{\it dz}\,{\it dy}\,{\it dx}& =&\int_{0}^{2\pi }\int_{0}^{1}\int_{0}^{2\sqrt{ 1-r^{2}}}\,{\it dz}\,r\,dr\,d\theta\\ &=&\int_{0}^{2\pi }\int_{0}^{1} \big[ z\big] _{0}^{2\sqrt{1-r^{2}}}r\,dr\,d\theta =\int_{0}^{2\pi }\int_{0}^{1}2r\sqrt{1-r^{2}}\ dr\,d\theta \\[5pt] & =&\int_{0}^{2\pi }\left[ -\dfrac{2}{3}(1-r^{2})^{3/2}\right] _{0}^{1}\,d\theta =\dfrac{2}{3}\int_{0}^{2\pi }d\theta =\dfrac{4\pi }{3} \end{array}$$

953

The value of the triple integral $\dfrac{4\pi }{3}$ equals the volume $V$ of the solid. That is, $$V=\dfrac{4\pi }{3} \hbox{ cubic units}$$