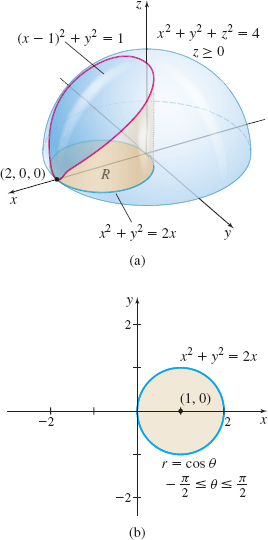
Finding the Volume of a Solid Using Cylindrical Coordinates
Find the volume of the solid enclosed by the hemisphere \( x^{2}+y^{2}+z^{2}=4,\) \(z\geq 0,\) and the cylinder \((x-1)^{2}+y^{2}=1\).
Because \(x^{2}+y^{2}\) appears in the equation of both the hemisphere and cylinder, we use cylindrical coordinates. The equation of the hemisphere is \[ \begin{array}{@{\hspace*{-1pc}}l@{\quad}rlrl} \hbox{Rectangular Coordinates:} &x^{2}+y^{2}+z^{2}&=4, z\geq 0\\ \hbox{Cylindrical Coordinates:} &r^{2}+z^{2}&=4, z\geq 0, \hbox{ or equivalently, } z=\sqrt{4-r^{2}} \end{array} \]
The equation of the region in the \(xy\)-plane above which the surface lies is given by: \[ \begin{eqnarray*} \hbox{Rectangular Coordinates:} & (x-1)^{2}+y^{2}&=1 & \\ & x^{2}+y^{2}&=2x & & \\ \hbox{Cylindrical Coordinates:} & r^{2}&=2( r\cos \theta ) & &{\color{#0066A7}{\hbox{$-\dfrac{\pi }{2} \leq \theta \leq \dfrac{\pi }{2}$}}} \\ & r&=2\cos \theta \end{eqnarray*} \]
See Figure 56(b).
The solid \(E\) whose volume we seek is given by \(0\leq z\leq \sqrt{4-r^{2}},\) \( 0\leq r\leq 2\cos \theta \), and \(-\dfrac{\pi }{2}\leq \theta \leq \dfrac{\pi }{2}.\) The volume \(V\) of the solid is \[ \begin{eqnarray*} V& =&\iiint\limits_{\kern-3ptE}{\it dV}=\iiint\limits_{\kern-3ptE}r\,dr\,d\theta \,{\it dz} \underset{\underset{{\color{#0066A7}{\hbox{Use symmetry}}}}{\color{#0066A7}{\uparrow}}}{=} 2\int_{0}^{\pi /2}\int_{0}^{2\cos \theta }\int_{0}^{\sqrt{4-r^{2}} }r\,{\it dz}\,dr\,d\theta \notag \\[-17pt] && \\[4pt] & =& 2 \int_{0}^{\pi /2}\int_{0}^{2\cos \theta }r\big[ z\big] _{0}^{\sqrt{4-r^{2}}}\,dr\,d\theta =2\int_{0}^{\pi /2}\int_{0}^{2\cos \theta }r( 4-r^{2}) ^{1/2}\,dr\,d\theta \\[4pt] &=&- \int_{0}^{\pi /2}\left[ \dfrac{2}{3}(4-r^{2})^{3/2}\right] _{0}^{2\cos \theta}\,d\theta \notag \\[4pt] &=&\dfrac{2}{3}\int_{0}^{\pi /2}[8-(4-4\cos ^{2}\theta )^{3/2}]\,d\theta =\dfrac{16}{3}\int_{0}^{\pi /2}(1-\sin ^{3}\theta )\,d\theta \\[4pt] &=&\dfrac{8\pi}{3} -\dfrac{32}{9} \hbox{cubic units } \end{eqnarray*} \]