Finding the Volume of a Solid Using Spherical Coordinates

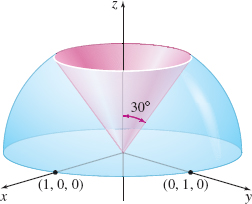
Find the volume of the solid that is removed from a hemisphere of radius 1 when it is cut by a cone that makes an angle of \(30^{\circ}\) with the positive \(z\)-axis.

Solution Figure 61 shows the part of the hemisphere cut by the cone, namely, the volume under the sphere and inside the cone. The upper surface is the hemisphere of radius \(r=1\); the lower surface is the \(xy\)-plane \((z=0)\). The angle \(\theta\) ranges from \(0\) to \(2\pi\) and \(\phi\) ranges from \(0\) to \(\dfrac{\pi}{6}.\) \[ 0\leq \rho \leq 1\qquad 0\leq \theta \leq 2\pi \qquad 0\leq \phi \leq \dfrac{\pi }{6} \]

Then the volume \(V\) of the solid is \[ \begin{eqnarray*} V &=&\iiint\limits_{E}\,\rho ^{2}\sin \phi \,d\rho \,d\theta \,d\phi =\int_{0}^{\pi /6}\int_{0}^{2\pi}\int_{0}^{1}\rho ^{2}\sin \phi \,d\rho \,d\theta \,d\phi\\ &=&\int_{0}^{\pi /6}\int_{0}^{2\pi}\left[\int_{0}^{1}\rho ^{2}d\rho \right] \sin\, \phi\, d\theta \,d\phi \notag \\ &=&\int_{0}^{\pi /6}\int_{0}^{2\pi }\left[ \dfrac{\rho ^{3}}{3}\right] _{0}^{1}\,d\theta \sin \phi \,d\phi =\int_{0}^{\pi /6}\left[\int_{0}^{2\pi } \dfrac{1}{3}d\theta \right] \sin \phi \,d\phi \notag \\ &=&\dfrac{2\pi}{3}\int_{0}^{\pi /6}\sin \phi \,d\phi =\left. \dfrac{2\pi }{3 }(-\cos \phi) \right] _{0}^{\pi /6}=\dfrac{2\pi }{3}\left( 1- \dfrac{\sqrt{3}}{2}\right) \end{eqnarray*} \]